浙教版2019-2020学年初中数学九年级上学期期末复习专题7 圆内接四边形
试卷更新日期:2019-12-18 类型:复习试卷
一、单选题
-
1. 四边形ABCD内接于⊙O,则∠A∶∠B∶∠C∶∠D的值可以是( )
A、2∶3∶4∶5 B、2∶4∶3∶5 C、2∶5∶3∶4 D、2∶3∶5∶42. 如图所示A、B、C、D四点在⊙O上的位置,其中 =180°,且 = , = .若阿超在 上取一点P,在 上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )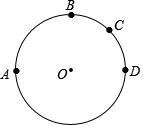 A、Q点在 上,且 > B、Q点在 上,且 < C、Q点在 上,且 > D、Q点在 上,且 <3. 已知下列命题:①抛物线y=3x2+5x-1与两坐标轴交点的个数为2个 ; ②相等的圆心角所对的弦相等; ③任何正多边形都有且只有一个外接圆; ④三角形的外心到三角形各顶点的距离相等; ⑤圆内接四边形对角相等;真命题的个数有( )A、1个 B、2个 C、3个 D、4个4. 如图,有一圆内接正八边形 ABCDEFGH,若△ADE的面积为10,则正八边形 ABCDEFGH的面积为( )
A、Q点在 上,且 > B、Q点在 上,且 < C、Q点在 上,且 > D、Q点在 上,且 <3. 已知下列命题:①抛物线y=3x2+5x-1与两坐标轴交点的个数为2个 ; ②相等的圆心角所对的弦相等; ③任何正多边形都有且只有一个外接圆; ④三角形的外心到三角形各顶点的距离相等; ⑤圆内接四边形对角相等;真命题的个数有( )A、1个 B、2个 C、3个 D、4个4. 如图,有一圆内接正八边形 ABCDEFGH,若△ADE的面积为10,则正八边形 ABCDEFGH的面积为( )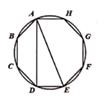 A、40 B、50 C、60 D、805. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )
A、40 B、50 C、60 D、805. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )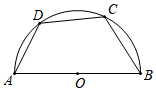 A、 B、 C、 D、6. 如图,四边形 内接于⊙ , 交 的延长线于点 ,若 平分 , ,则 ( )
A、 B、 C、 D、6. 如图,四边形 内接于⊙ , 交 的延长线于点 ,若 平分 , ,则 ( ) A、 B、 C、 D、7. 如图,四边形ABCD是⊙O的内接四边形,已知∠BCD=110°,则∠BOD的度数为( )
A、 B、 C、 D、7. 如图,四边形ABCD是⊙O的内接四边形,已知∠BCD=110°,则∠BOD的度数为( ) A、70° B、90° C、110° D、140°8. 已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )
A、70° B、90° C、110° D、140°8. 已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )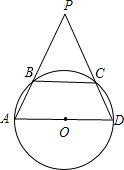 A、25π B、16π C、15π D、13π9. 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
A、25π B、16π C、15π D、13π9. 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( ) A、50° B、60° C、80° D、100°10. 如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
A、50° B、60° C、80° D、100°10. 如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )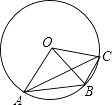 A、∠OBA=∠OCA B、四边形OABC内接于⊙O C、AB=2BC D、∠OBA+∠BOC=90°
A、∠OBA=∠OCA B、四边形OABC内接于⊙O C、AB=2BC D、∠OBA+∠BOC=90°二、填空题
-
11. ⊙O是△ABC的外接圆,OD⊥BC于D,且∠BOD=48°,∠BAC= .
12. 已知点A,B,C在⊙O上(点C不与A,B重合), , 则 = °.13. 如图,四边形ABCD内接于⊙O,连结AC,若∠BAC=35°,∠ACB=40°,则∠ADC=°.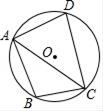 14. ⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为 ,M是圆上一点,∠BMO=150°.则圆心C的坐标为 .
14. ⊙C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为 ,M是圆上一点,∠BMO=150°.则圆心C的坐标为 .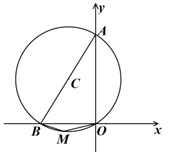 15. 在圆内接四边形ABCD中,∠D-∠B=40°,则∠B=度.16. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为.
15. 在圆内接四边形ABCD中,∠D-∠B=40°,则∠B=度.16. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为.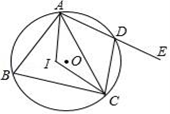
三、解答题
-
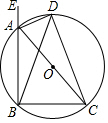
17. 如图,四边形ABCD是 的内接四边形,DB=DC求证:∠CAD=∠EAD.
 18. 如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
18. 如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑) 19. 如图,已知四边形ABCD内接于圆O,∠A=105°,BD=CD.
19. 如图,已知四边形ABCD内接于圆O,∠A=105°,BD=CD.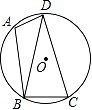 (1)、求∠DBC的度数;(2)、若⊙O的半径为3,求 的长.20. 如图,已知ʘO是Rt△ABC的外接圆,点D是ʘO上的一个动点,且C,D位于AB的两侧,联结AD,BD,过点C作CE⊥BD,垂足为E。延长CE交ʘO于点F,CA,FD的延长线交于点P。
(1)、求∠DBC的度数;(2)、若⊙O的半径为3,求 的长.20. 如图,已知ʘO是Rt△ABC的外接圆,点D是ʘO上的一个动点,且C,D位于AB的两侧,联结AD,BD,过点C作CE⊥BD,垂足为E。延长CE交ʘO于点F,CA,FD的延长线交于点P。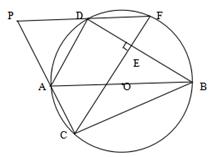
求证:
(1)、弧AF=弧DC.(2)、△PAD是等腰三角形.21. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E. (1)、若∠ADC=86°,求∠CBE的度数;(2)、若AC=EC,求证:AD=BE22. 如图,四边形ABCD是⊙O的内接四边形,BD是∠ABC的角平分线,过点D分别作DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)、若∠ADC=86°,求∠CBE的度数;(2)、若AC=EC,求证:AD=BE22. 如图,四边形ABCD是⊙O的内接四边形,BD是∠ABC的角平分线,过点D分别作DE⊥AB,DF⊥BC,垂足分别为E、F.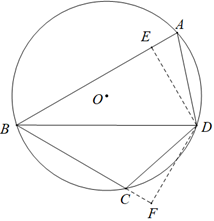 (1)、求证△AED≌△CFD;(2)、若AB=10,BC=8,∠ABC=60°,求BD的长度.23. 如图,⊙ 的内接四边形ABCD两组对边的延长线分别相交于点E、F。
(1)、求证△AED≌△CFD;(2)、若AB=10,BC=8,∠ABC=60°,求BD的长度.23. 如图,⊙ 的内接四边形ABCD两组对边的延长线分别相交于点E、F。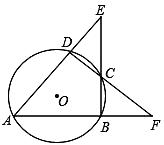 (1)、若∠E=∠F时,求证:∠ADC=∠ABC;(2)、若∠E=∠F=42°时,求∠A的度数;(3)、若∠E=α,∠F=β,且。α≠β.请你用含有α、β的代数式表示∠A的大小.24. 定义:有一个角是其对角一半的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.(1)、如图1,若四边形ABCD是圆美四边形,求美角∠A的度数.
(1)、若∠E=∠F时,求证:∠ADC=∠ABC;(2)、若∠E=∠F=42°时,求∠A的度数;(3)、若∠E=α,∠F=β,且。α≠β.请你用含有α、β的代数式表示∠A的大小.24. 定义:有一个角是其对角一半的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.(1)、如图1,若四边形ABCD是圆美四边形,求美角∠A的度数.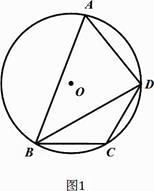 (2)、在(1)的条件下,若⊙O的半径为5.
(2)、在(1)的条件下,若⊙O的半径为5.①求BD的长.
②如图2,在四边形ABCD中,若CA平分∠BCD,则BC+CD的最大值是 .
 (3)、在(1)的条件下,如图3,若AC是⊙O的直径,请用等式表示线段AB,BC,CD之间的数量关系,并说明理由.
(3)、在(1)的条件下,如图3,若AC是⊙O的直径,请用等式表示线段AB,BC,CD之间的数量关系,并说明理由.