浙教版2019-2020学年初中数学九年级上学期期末复习专题6 圆心角与圆周角定理
试卷更新日期:2019-12-18 类型:复习试卷
一、单选题
-
1. 下列四条圆弧与直角三角板的位置关系中,可判断其中的圆弧为半圆的是( )A、
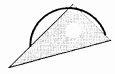 B、
B、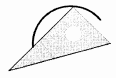 C、
C、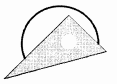 D、
D、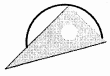 2. 如果两条弦相等,那么( )A、这两条弦所对的圆心角相等 B、这两条弦所对的弧相等 C、这两条弦所对的弦心距相等 D、以上说法都不对3. 如图,AD是△ABC外接圆的直径.若∠B=64°,则∠DAC等于( )
2. 如果两条弦相等,那么( )A、这两条弦所对的圆心角相等 B、这两条弦所对的弧相等 C、这两条弦所对的弦心距相等 D、以上说法都不对3. 如图,AD是△ABC外接圆的直径.若∠B=64°,则∠DAC等于( )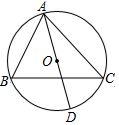 A、26° B、28° C、30° D、32°4. 如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )
A、26° B、28° C、30° D、32°4. 如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )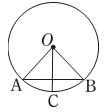 A、40° B、45° C、50° D、60°5. 如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为( )
A、40° B、45° C、50° D、60°5. 如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为( )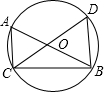 A、
A、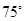 B、
B、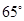 C、
C、 D、
D、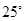 6. 如图,以AB为直径的半圆上有一点C,∠C=25°,则 的度数为( )
6. 如图,以AB为直径的半圆上有一点C,∠C=25°,则 的度数为( )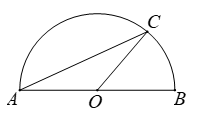 A、25° B、30° C、50° D、65°7. 如图,点A,B,C在⊙O上,∠AOB=70°,则∠ACB的度数是( )
A、25° B、30° C、50° D、65°7. 如图,点A,B,C在⊙O上,∠AOB=70°,则∠ACB的度数是( ) A、70° B、30° C、35° D、40°8. 如图,C,D是⊙O上位于直径AB异侧的两点,若∠ACD=20°,则∠BAD的度数是( )
A、70° B、30° C、35° D、40°8. 如图,C,D是⊙O上位于直径AB异侧的两点,若∠ACD=20°,则∠BAD的度数是( )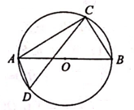 A、40° B、50° C、60° D、70°9. 如图,已知 的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为( )
A、40° B、50° C、60° D、70°9. 如图,已知 的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为( )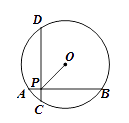 A、3 B、4 C、 D、10. 如图,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论中不正确的是( )
A、3 B、4 C、 D、10. 如图,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论中不正确的是( )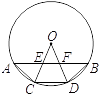 A、OE=OF B、弧AC=弧BD C、AC=CD=DB D、CD∥AB
A、OE=OF B、弧AC=弧BD C、AC=CD=DB D、CD∥AB二、填空题
-
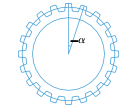
11. 如图的齿轮有30个齿,每两齿之间的间隔相等,则相邻两齿间的圆心角 等于度.
 12. 如图,AB为 的直径,CD为 的弦,∠BCD=34°,则∠ABD=.
12. 如图,AB为 的直径,CD为 的弦,∠BCD=34°,则∠ABD=. 13. 如图,在⊙ 中,半径 垂直于弦 ,点 在圆上且 ,则 的度数为 .
13. 如图,在⊙ 中,半径 垂直于弦 ,点 在圆上且 ,则 的度数为 .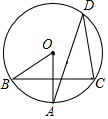 14. 一条弦把圆分为2∶3的两部分,那么这条弦所对的圆周角度数为。15. 如图,四边形 ABCD 内接于⊙O ,AB 为⊙O 的直径,点 C 为弧 BD 的中点.若∠DAB=40°,则∠ABC= .
14. 一条弦把圆分为2∶3的两部分,那么这条弦所对的圆周角度数为。15. 如图,四边形 ABCD 内接于⊙O ,AB 为⊙O 的直径,点 C 为弧 BD 的中点.若∠DAB=40°,则∠ABC= . 16. 如图,在矩形ABCD中,AB=6,AD=8,E是BC上的一动点(不与点B、C重合).连接AE,过点D作DF⊥AE,垂足为F,则线段BF长的最小值为.
16. 如图,在矩形ABCD中,AB=6,AD=8,E是BC上的一动点(不与点B、C重合).连接AE,过点D作DF⊥AE,垂足为F,则线段BF长的最小值为.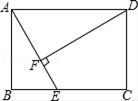
三、解答题
-
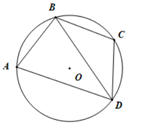
17. 已知:如图,四边形ABCD的顶点都在⊙O上,BD平分∠ADC,且BC=CD. 求证: AB=CD.
 18. 如图, 的一条弦分圆周长为1:4两部分.试求弦AB所对的圆心角和圆周角的度数(画出图形并给出解答).
18. 如图, 的一条弦分圆周长为1:4两部分.试求弦AB所对的圆心角和圆周角的度数(画出图形并给出解答).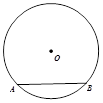 19. 已知:如图,A,B,C,D是⊙O上的点,且AB=CD,求证:∠AOC=∠BOD.
19. 已知:如图,A,B,C,D是⊙O上的点,且AB=CD,求证:∠AOC=∠BOD.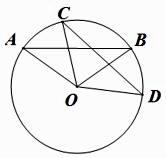 20. 如图,把一个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线CP绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB重合,就停止旋转。在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.
20. 如图,把一个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线CP绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB重合,就停止旋转。在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE. (1)、设旋转x秒后,点E处的读数为y,则y与x的函数关系式.(2)、当CP旋转.秒时,△BCE是等腰三角形。21. 如图,小高家的院子里有三棵树A、B、C,小高想建一个圆形花坛,使三棵树都在花坛的边上.
(1)、设旋转x秒后,点E处的读数为y,则y与x的函数关系式.(2)、当CP旋转.秒时,△BCE是等腰三角形。21. 如图,小高家的院子里有三棵树A、B、C,小高想建一个圆形花坛,使三棵树都在花坛的边上.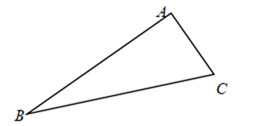 (1)、请帮小高把花坛的位置画出来(用尺规作图法,保留作图痕迹,不要求写作法);(2)、若△ABC中,AB=8,AC=6,∠BAC=90°,试求小高家的圆形花坛的面积.22. 如图,在平面直角坐标系中,以点M(0, )为圆心,以 长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
(1)、请帮小高把花坛的位置画出来(用尺规作图法,保留作图痕迹,不要求写作法);(2)、若△ABC中,AB=8,AC=6,∠BAC=90°,试求小高家的圆形花坛的面积.22. 如图,在平面直角坐标系中,以点M(0, )为圆心,以 长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.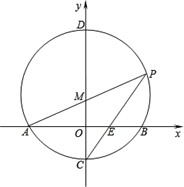 (1)、求点C.P的坐标;(2)、求证:BE=2OE.23. 如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,连接AC、FC.
(1)、求点C.P的坐标;(2)、求证:BE=2OE.23. 如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,连接AC、FC.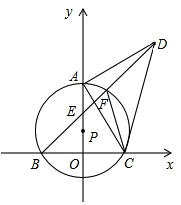 (1)、求证:∠ACF=∠ADB;(2)、若点A到BD的距离为m,BF+CF=n,求线段CD的长;(3)、当⊙P的大小发生变化而其他条件不变时, 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.24. 一节数学课后,老师布置了一道课后练习题:
(1)、求证:∠ACF=∠ADB;(2)、若点A到BD的距离为m,BF+CF=n,求线段CD的长;(3)、当⊙P的大小发生变化而其他条件不变时, 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.24. 一节数学课后,老师布置了一道课后练习题:如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,CE=CB,BE分别交CD、AC于点F、G.求证:CF=FG。
 (1)、初步尝试
(1)、初步尝试本题证明的思路可用下列框图表示:
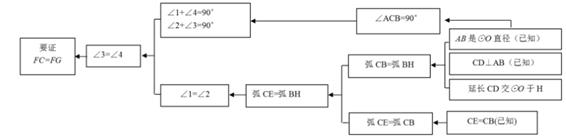
根据上述思路,请你完整地书写本题的证明过程。
(2)、类比探究如图,若点C和点E在AB的两侧,BE、CA的延长线交于点G,CD的延长线交BE于点F,其余条件不变,(1)中的结论还成立吗?请说明理由;
 (3)、延伸拓展
(3)、延伸拓展在(2)的条件下,若BG=26,BD-DF=7,求BC的长。