浙教版2019-2020学年初中数学九年级上学期期末复习专题5 垂径定理
试卷更新日期：2019-12-18 类型：复习试卷
一、单选题
-
1. 如图，AB是⊙O的直径，弦CD⊥AB于点E ， OC=5cm，CD=8cm，则AE的长为（ ）
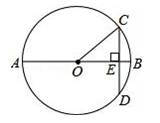A、8cm B、5cm C、3cm D、2cm2. 如图，AB为⊙O的弦，过点O作AB的垂线，交AB于点C，交⊙O于点D，已知⊙O的直径为10，CD=2，则AB的长为（ ）
A、4 B、6 C、8 D、103. 如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，距拖拉机中心50米的范围内均会受到噪音影响，已知有两台相距40米的拖拉机正沿ON方向行驶，它们的速度均为10米/秒，则这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间为（ ）
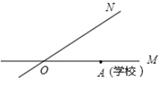A、6秒 B、8秒 C、10秒 D、18秒4. 如图，在半径为3的⊙O中，B是劣弧AC的中点，连接AB并延长到D，使BD＝AB，连接AC、BC、CD，如果AB＝2，那么CD等于（ ）
A、2 B、1 C、 D、5. 如图，⊙O的直径CD垂直于弦AB于点E，且CE=2，DE=8，则AB的长为( ）
A、2 B、4 C、6 D、86. 一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D，现测得AB=8dm，DC=2dm，则圆形标志牌的半径为（ ）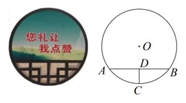
A、6dm B、5dm C、4dm D、3dm7. 如图，将一把两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D、E，量出半径OC=5cm，弦DE=8cm，则直尺的宽度是（ ）
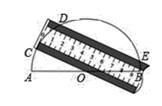A、4cm B、3cm C、2cm D、1cm8. 如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE∥AC交半圆O于点E，过点E作EF⊥AB于F．若AC=2，则OF的长为（ ）
A、 B、 C、1 D、29. 已知点E在半径为5的⊙O上运动，AB是⊙O的弦且AB=8，则使△ABE的面积为8 的点E共有（ ）个
A、 1 B、2 C、3 D、4二、填空题
-
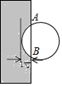
10. 过⊙O内一点P的最长弦长为10cm，最短弦长为8cm，那么OP的长为cm．11. 《九章算术》中记载有一问题“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”小辉同学根据原文题意，画出圆材截面图如图所示，已知：锯口深为1寸，锯道AB＝1尺（1尺＝10寸），则该圆材的直径为寸．
12. 为测量一铁球的直径，将该铁球放入工件槽内，测得有关数据如图所示（单位：cm），则该铁球的直径为
13. 如图，以G(0，1)为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C，D两点，点E为⊙O上一动点，CF⊥AE于F，则弦AB的长度为；点E在运动过程中，线段FG的长度的最小值为.
14. 如图，AB是⊙O的直径，C、D是⊙O上的两个动点(点C、D不与A、B重合)，在运动过程中弦CD始终保持不变，F是弦CD的中点，过点C作CE⊥AB于点E．若CD=5，AB=6，当EF取得最大值时，CE的长度为 。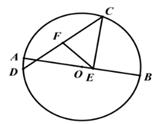
15. 如图，CD为⊙O的直径，弦AB⊥CD，垂足为M，若AB＝8，OM：CM＝3：8，则⊙O的周长为 ．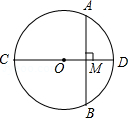
三、解答题
-
16. 如图所示，已知⊙O的直径AB垂直弦CD于点E，连接CO并延长交AD于点F．若CF⊥AD，AB＝2，求CD的长．
17. 如图，AB是半圆的直径，0是圆心，C是半圆上一点，D是弧AC的中点，0D交弦AC于E，连接BE．若AC=8，DE=2，求BE的长度．
18. 已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图所示）．
(1)、求证：AC=BD；
(2)、若大圆的半径R=10，小圆的半径r=8，且圆心O到直线AB的距离为6，求AC的长
19. 如图，有一座圆弧形拱桥，桥下水面宽度AB为12m，拱高CD为4m.
(1)、求拱桥的半径；(2)、有一艘宽为5m的货船，船舱顶部为长方形，并高出水面3.4m，则此货船是否能顺利通过此圆弧形拱桥，并说明理由；20. 某居民小区一处圆柱形的输水管破裂，维修人员为更新管道，需确定管道圆形截面的半径，如图所示是水平放置的破裂管道有水部分的截面．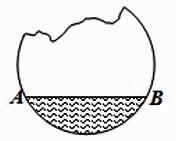
(1)、请你补全这个输水管道的圆形截面（要求：保留作图痕迹，标出圆心O）；
(2)、若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．
21. 如图，公路MN和村路PQ在P处交汇，且∠QPN=30°，点A处有一所中学，AP=160m．假设拖拉机行驶时，周围100m以内会受到噪声的影响，那么拖拉机在公路MN上沿PN方向行驶时，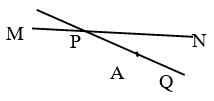
(1)、学校是否会受到噪声影响？请说明理由；(2)、如果受影响，已知拖拉机的速度为18km/h时，那么学校受影响的时间为多少秒？22. 如图，AB是⊙O的直径，弦CD交AB于点E，OF⊥AC于点F，
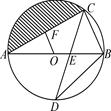(1)、请探索OF和BC的关系，并说明理由；(2)、若∠D＝30°，BC＝1时，求圆中阴影部分的面积．(结果保留π)23. 如图，⊙O的直径AB=20，P是AB上（不与点A，B重合）的任一点，点C，D为⊙O上的两点，若∠APD=∠BPC，则称∠DPC为直径AB的“回旋角”，利用圆的对称性可知：“回旋角”∠DPC的度数与弧CD的度数相等.
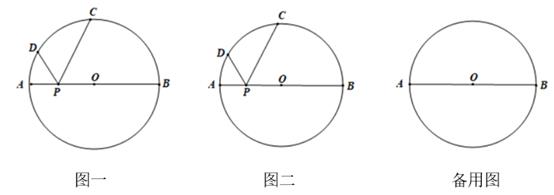(1)、若∠DPC为直径AB的“回旋角”，且∠DPC=100°，求∠APD的大小；(2)、若直径AB的“回旋角”为90°，且△PCD的周长为 ，求AP的长.