浙教版2019-2020学年初中数学九年级上学期期末复习专题3 圆的认识
试卷更新日期：2019-12-18 类型：复习试卷
一、单选题
-
1. 下列命题：①直径相等的两个圆是等圆；②等弧是长度相等的弧；③圆中最长的弦是通过圆心的弦； ④一条弦把圆分为两条弧，这两条弧不可能是等弧.其中真命题是 （ ）A、①③ B、①③④ C、①②③ D、②④2. 如图，在Rt△ABC中，∠ACB=90°，AC=3，AB=5，CD是斜边AB上的中线，以AC为直径作O，设线段CD的中点为P，则点P与O的位置关系是（ ）
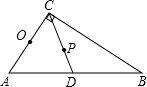A、点P在O外 B、点P在O上 C、点P在O内 D、无法确定3. 给定下列条件可以确定一个圆的是（ ）A、已知圆心 B、已知半径 C、已知直径 D、不在同一直线上三点4. 下列四个命题中，①圆的对称轴是直径；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．正确的有（ ）A、4个 B、3个 C、2个 D、1个5. 已知⊙O的半径为2，点P在⊙O内，则OP的长可能是（ ）A、1 B、2 C、3 D、46. 若圆的半径是 ，圆心的坐标是 ，点 的坐标是 ，则点 与 的位置关系是（ ）A、点P在⊙O外 B、点P在⊙O内 C、点P在⊙O上 D、点P在⊙O外或⊙O上7. 如图，在8×8正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（ ）
A、点E B、点F C、点G D、点H8. 抢凳子是小时候常玩的游戏，人围成圈将凳子放在中间，主持人开始敲鼓，此时人围着凳子按同一方向转圈.当敲击声停止时，就要抢坐在凳子上，因为凳子数量少于玩游戏的总人数，未抢坐到凳子上的玩家淘汰下场.现在甲、乙、丙3位同学准备玩抢凳子的游戏，谁先抢坐到凳子上谁获胜.如图，三人已站定，主持人要在他们中间放一个凳子，为使游戏公平，凳子应放在图中三角形的 （ ）
A、三条高的交点 B、重心 C、内心 D、外心9. 如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点△ABC的外部，则下列叙述正确的是（ ）．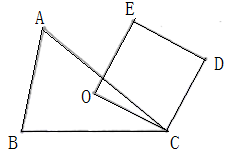
A、D是△AEB的外心，O是△AED的外心 B、O不是△AEB的外心，O不是△AED的外心 C、D不是△AEB的外心，O是△AED的外心 D、O是△AEB的外心，O不是△AED的外心10. 小明不慎把家里的圆形镜子打碎了，其中三块碎片如图所示，三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是（ ）
A、① B、② C、③ D、均不可能二、填空题
-
11. 战国时期的数学家墨子撰写的《墨经》一书中，就有“圆，一中同长也”的记载，这句话中的“中”字的意思可以理解为12. 若⊙O的半径为6cm，则⊙O中最长的弦为厘米．
13. 两直角边长分别为6和8的直角三角形的外接圆直径是 ．
14. 如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），点P在以D（3，5）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的最小值是.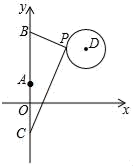
15. 如图，Rt△ABC中，∠ACB=90°，AC=4，BC=3，CD是斜边AB上的高线，以点C为圆心，2.5为半径作圆，则点D在圆（填“外”，“内”，“上”）．
16. 如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C在格点（两条网格线的交点叫格点）上，以点O为原点建立直角坐标系，则过A，B，C三点的圆的圆心坐标为 ．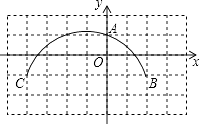
三、解答题
-
17. 已知：如图，在⊙O中，弦AB=CD．求证：∠AOC =∠BOD．
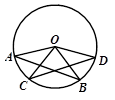18. 如图，已知△ABC中，AC=6，∠ABC=45°.
(1)、用直尺和圆规作出△ABC的外接圆（保留作图痕迹，写出结论，不写画法）；(2)、求出△ABC的外接圆半径.19. 如图，点O是线段AB的中点，根据要求完成下题：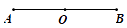
(1)、在图中补画完成：第一步，以A B为直径的画出⊙O；
第二步，以B为圆心，以BO为半径画圆弧，交⊙O于点C，连接点CA，CO；
(2)、设AB=6，求扇形AOC的面积.（结果保留π）20. 已知：如图，△ABC中， ， cm， cm，CM是中线，以C为圆心，以 cm长为半径画圆，则点A、B、M与⊙C的关系如何？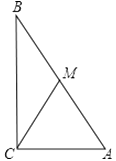
21. 某体育中心要修建一处公共服务设施，使它到三所运动员公寓A，B，C 的距离相等．
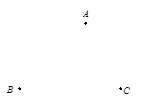(1)、若三所运动员公寓A、B、C的位置如图所示，请你在图中确定这处公共服务设施（用点P表示）的位置；(2)、若∠BAC＝90º，且AB=8，AC=6，求△ABC的外接圆的面积。22. 如图， 是 的边 的中点，过 延长线上的点 作 的垂线 ， 为垂足， 与 的延长线相交于点 ，点 在 上， ， ∥ .
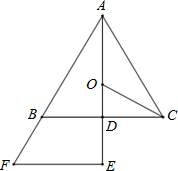(1)、证明： ；(2)、证明：点 是 的外接圆的圆心；23. 如图，在平面直角坐标系中，直线l与x轴相交于点M，与y轴相交于点N，Rt△MON的外心为点A（ ，﹣2），反比例函数y= （x＞0）的图象过点A．
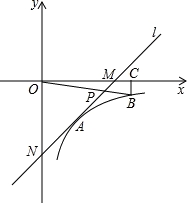(1)、求直线l的解析式；(2)、在函数y= （x＞0）的图象上取异于点A的一点B，作BC⊥x轴于点C，连接OB交直线l于点P．若△ONP的面积是△OBC面积的3倍，求点P的坐标．24. 如图，一次函数y＝kx﹣2（k≠0）的图象与y轴交于点A，与反比例函数y＝ （x＞0）的图象交于点B（3，b）．点C是线段AB上的动点（与点A、B不重合），过点C且平行于y轴的直线CD交这个反比例函数的图象于点D，O为坐标原点．
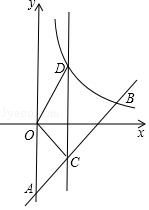(1)、求△OCD面积为 时，点D的坐标；(2)、求△OCD面积的最大值；(3)、当△OCD面积最大时，以点O为圆心，r为半径画⊙O，是否存在r的值，使得A、B、C、D四个点中恰好有2个在圆内？如果存在，求出r的取值范围；如果不存在，请说明理由．