浙江省台州市温岭市2019-2020学年七年级上学期期中数学试题
试卷更新日期:2019-12-18 类型:期中考试
一、单选题
-
1. 如果“盈利5%”记作+5%,那么﹣3%表示( )A、少赚3% B、亏损-3% C、盈利3% D、亏损3%2. 如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )A、
 B、
B、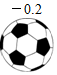 C、
C、 D、
D、 3. 2019年1月3日,嫦娥4号月球探测器在月球背面的预定着陆区中顺利着陆,地球与月球之间的平均距离大约为384000km , 384000用科学记数法表示为( )A、3.84×103 B、3.84×104 C、3.84×105 D、3.84×1064. 下列各数中,互为相反数的是( )A、﹣(﹣4)和|﹣4| B、﹣|﹣2|和﹣(+2) C、﹣(﹣3)和﹣|﹣3| D、﹣12和﹣15. 在-1, +7.5, 0, , -0.9, 15中.负分数共有( ).A、l个 B、2个 C、3个 D、4个6. 下列说法正确的是( )A、单项式a的系数是0 B、单项式﹣ 的系数和次数分别是﹣3和2 C、x2﹣2x+25是五次三项式 D、单项式﹣3πxy2z3的系数和次数分别是﹣3π和67. 已知 ,那么下列关系正确的是( )A、 B、 C、 D、8. 若 ,则 的值可表示为( )A、 B、 C、 D、9. 当x=4时,多项式ax7+bx5+cx3﹣3的值为-4,则当x=﹣4时,该多项式的值为( )A、4 B、-3 C、-2 D、答案不确定10. 如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l . 若知道l的值,则不需要测量就能知道周长的正方形的标号为( )
3. 2019年1月3日,嫦娥4号月球探测器在月球背面的预定着陆区中顺利着陆,地球与月球之间的平均距离大约为384000km , 384000用科学记数法表示为( )A、3.84×103 B、3.84×104 C、3.84×105 D、3.84×1064. 下列各数中,互为相反数的是( )A、﹣(﹣4)和|﹣4| B、﹣|﹣2|和﹣(+2) C、﹣(﹣3)和﹣|﹣3| D、﹣12和﹣15. 在-1, +7.5, 0, , -0.9, 15中.负分数共有( ).A、l个 B、2个 C、3个 D、4个6. 下列说法正确的是( )A、单项式a的系数是0 B、单项式﹣ 的系数和次数分别是﹣3和2 C、x2﹣2x+25是五次三项式 D、单项式﹣3πxy2z3的系数和次数分别是﹣3π和67. 已知 ,那么下列关系正确的是( )A、 B、 C、 D、8. 若 ,则 的值可表示为( )A、 B、 C、 D、9. 当x=4时,多项式ax7+bx5+cx3﹣3的值为-4,则当x=﹣4时,该多项式的值为( )A、4 B、-3 C、-2 D、答案不确定10. 如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l . 若知道l的值,则不需要测量就能知道周长的正方形的标号为( ) A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
11. 0的相反数是;0.5的倒数是;x2+2x-3的常数项是 .12. 比较大小<用“>"或“<"表示):13. 近似数8.28万精确到位.14. 规定符号⊗的意义为:a⊗b=ab﹣a﹣b+1,那么﹣2⊗5= .15. 飞机顺风时速度为x千米/时,风速为y千米/时,则飞机逆风速度为千米/时.16. 已知a、b互为相反数,m、n互为倒数,x的绝对值为2,则﹣2mn+ ﹣x= .17. 如图,数轴上点A表示的数为a,化简:|a-3|-2|a+1|= .
 18. 一个三位数为x , 一个两位数为y , 把这个三位数放在两位数的左边得到一个五位数M , 把这个两位数放在三位数的左边又可以得到一个五位数N , 则M﹣N=(结果用含x , y的式子表示).19. 在数学中,为了简便,记 ,1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n﹣1)×(n﹣2)×…×3×2×1,则 .20. 如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1 , 第2幅图形中“●”的个数为a2 , 第3幅图形中“●”的个数为a3 , …,以此类推,则 的值为
18. 一个三位数为x , 一个两位数为y , 把这个三位数放在两位数的左边得到一个五位数M , 把这个两位数放在三位数的左边又可以得到一个五位数N , 则M﹣N=(结果用含x , y的式子表示).19. 在数学中,为了简便,记 ,1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n﹣1)×(n﹣2)×…×3×2×1,则 .20. 如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1 , 第2幅图形中“●”的个数为a2 , 第3幅图形中“●”的个数为a3 , …,以此类推,则 的值为
三、解答题
-
21. 计算(1)、(﹣14)﹣5+(﹣18)﹣(﹣34)(2)、(3)、(4)、22. 化简:(1)、2x2﹣3x+7﹣4x2+3x+1(2)、2(8xy﹣x2+y2)﹣3(x2﹣2y2+8xy)23. 先化简,再求值:2(a2b+ab2)﹣3(a2b﹣1)﹣2ab2﹣4,其中a=2019,b= .24. 七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现有甲、乙两家商店出售两种同样的笔记本和钢笔.他们的定价相同:笔记本定价为每本25元,钢笔每支定价6元,但是他们的优惠方案不同,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.已知七年级需笔记本20本,钢笔x支(大于20支).问:(1)、在甲店购买需付款元,在乙店购买需付款元;(2)、若x=30,通过计算说明此时到哪家商店购买较为合算?(3)、当x=40时,请设计一种方案,使购买最省钱?算出此时需要付款多少元?25. 定义:如果10b=n , 那么称b为n的劳格数,记为b=d(n).(1)、根据劳格数的定义,可知:d(10)=1,d(102)=2,那么:d(103)= .(2)、劳格数有如下运算性质:若m , n为正数,则d(mn)=d(m)+d(n); d( )=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= , 则d( )= , d( )= .26. [背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b;线段AB的中点M表示的数为 .
[问题情境]
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).

[综合运用]
(1)、运动开始前,A、B两点的距离为;线段AB的中点M所表示的数 .(2)、点A运动t秒后所在位置的点表示的数为;点B运动t秒后所在位置的点表示的数为;(用含t的代数式表示)(3)、它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?(4)、若A,B按上述方式继续运动下去,线段AB的中点M能否与原点重合?若能,求出运动时间,并直接写出中点M的运动方向和运动速度;若不能,请说明理由.(当A,B两点重合,则中点M也与A,B两点重合)