浙江省温州市瑞安市六校联盟2019-2020学年八年级上学期期中数学试卷
试卷更新日期：2019-12-18 类型：期中考试
一、单选题
-
1. 下列各校的图标中，是轴对称图形的（ ）.A、
B、
C、
D、
2. 下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是（ ）A、1,2,1 B、1,2,2 C、1,2,3 D、1,2,43. 下列语句是命题（ ）.A、将27开立方 B、任意三角形的三条中线相交于一点吗? C、锐角小于直角 D、做一条直线和已知直线垂直4. 在△ABC中，若∠A=15°，∠B= 150°，则△ABC（ ）A、等腰三角形. B、等边三角形 C、直角三角形 D、锐角三角形5. 下列命题为假命题的是（ ）.A、三条边分别对应相等的两个三角形全等 B、三角形的一个外角大于与它相邻的内角 C、角平分线上的点到角两边的距离相等 D、等边三角形的三条角平分线、三条中线、三条高分别交于一点6. 如图，已知∠1=∠2， AC=AE，下列条件无法确定△ABC≌△ADE的（ ） .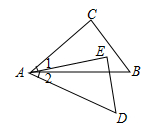
A、∠C=∠E B、BC=DE C、AB=AD D、∠B=∠D7. 下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线，则对应选项中作法错误的是（ ）
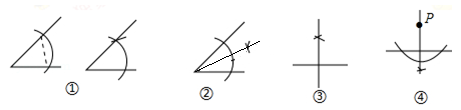A、① B、② C、③ D、④8. 如图，射线AD，BE，CF构成∠1，∠2，∠3，则∠1+∠2+∠3=（ ）
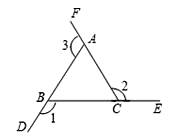A、180° B、360° C、540° D、无法确定9. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（ ）
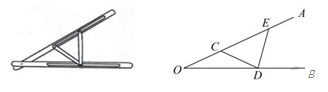A、60° B、65° C、75° D、80°10. 如图，在△ABC中，∠ABC=45° ， BC=4，以AC为直角边，点A为直角顶点向△ABC的外侧作等腰直角三角形ACD，连接BD，则△DBC的面积为（ ） .
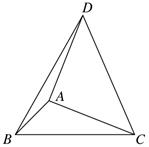A、8 B、10 C、4 D、8二、填空题
-
11. “两直线平行，内错角相等”的逆命题是 ．12. 如图，点D、E分别在线段AB、AC上，BE、CD相交于点Ｏ，AE＝AD要使△ABE≌△ACD，需添加一个条件是（只要写一个条件）．
13. 已知等腰三角形的两边长分别为1和3，则周长等于.14. 如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE＝1，∠E＝30°，则BC＝.
15. 如图，分别以Rt△ABC为边长向外作等边三角形，若AC=2，∠ACB=90°，∠ABC=30°，则三个等边三角形的面积之和是.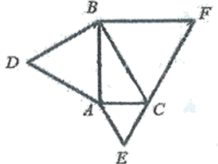
16. 如图，在Rt△ABC中，∠ACB=90° ，AC=3，BC=6，点D在AB上，AD=AC， AF⊥CD交CD于点E，交CB于点F，则CF的长是.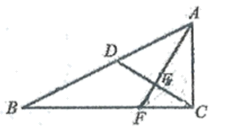
三、解答题
-
17. 如图，直线l表示一条公路，点A， B表示两个村庄.现要在公路l上按以下要求建一个加油站，请在图中用点P表示加油站的位置. (不写作法，保留作图痕迹)
(1)、在图甲中标出加油站的位置，使得加油站到A， B两个村庄的距离相等.(2)、在图乙中标出加油站的位置，使得加油站到A， B两个村庄的距离之和最小，18. 如图，△ABC中，∠ABC=60°，∠ACB=50°，延长CB至点D，使DB=BA，延长BC至点E，使CE=CA，连接AD，AE. 求∠DAE的度数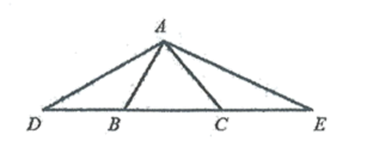
.19. 如图，在△ABC中，AB=AC ， ∠A=36°，BD平分∠ABC交AC于点D ．求证：AD=BC ．
20. 如图，CD是线段AB的垂直平分线，则∠CAD= ∠CBD．请说明理由：
解：∵CD是线段AB的垂直平分线，
∴AC= ▲ ， ▲ =BD．.
在△ACD和△BCD中，
. ▲ =BC，
AD= ▲ ，
CD=CD，
∴△ACD≌▲ （ ） .
∴∠CAD=∠CBD（ ）
21. 如图，Rt△ABC中，∠C=90°， 点D在AB上，且CD=BD．
(1)、求证：点D是AB的中点.(2)、以CD为对称轴将△ACD翻折至△A'CD，连接BA'，若∠DBC=a，求∠CB A'的度数.
