浙江省杭州市萧山区城区片六校2019-2020学年八年级上学期期中数学试卷
试卷更新日期：2019-12-18 类型：期中考试
一、单选题
-
1. 在△ABC中，∠A=75°，∠B=65°，则下列关于∠C的说法正确的是（ ）A、它等于40° B、它等于50° C、它是个直角 D、它是个钝角2. 等腰三角形的两边长分别为3和6，它的周长是（ ）A、12 B、14 C、15 D、12或153. 若 ，则下列式子中，错误的是（ ）A、 B、 C、 D、4. 对于命题“若 ，则 ”，能说明它属于假命题的反例是（ ）A、 B、 C、 D、5. 如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
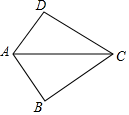A、CB＝CD B、∠BCA＝∠DCA C、∠BAC＝∠DAC D、∠B＝∠D＝90°6. 如图所示，在△ABC中，∠BAC=130°，AB的垂直平分线ME交BC于点M，交AB于点E，AC的垂直平分线NF交BC于点N，交AC于点F，则∠MAN为（ ）
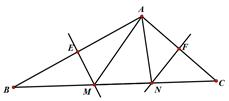A、80° B、70° C、60° D、50°7. 如图所示，在4×4的方格纸中有一个格点△ABC（每个小正方形的边长为1），下列关于它的描述中，正确的是（ ）
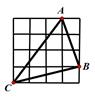A、三边长都是有理数 B、是等腰三角形 C、是直角三角形 D、面积为6.58. 甲在集市上先买了 只羊，平均每只 元，稍后又买了 只，平均每只羊 元，后来他以每只 元的价格把羊全卖给了乙，结果发现赔了钱，赔钱的原因是（ ）A、 B、 C、 D、与 、 大小无关9. 如图，小明（视为小黑点）站在一个高为10米的高台A上，利用旗杆OM顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B．那么小明在荡绳索的过程中离地面的最低点的高度MN是（ ）
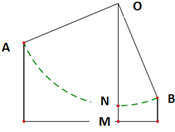A、2米 B、2.2米 C、2.5米 D、2.7米10. 如图，P是等边三角形ABC内一点，且PA=4，PB= ，PC=2，以下五个结论：①∠ BPC=120°；②∠APC=120°；③ ；④AB= ；⑤点P到△ABC三边的距离分别为PE，PF，PG，则有 其中正确的有（ ）
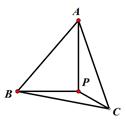A、4个 B、3个 C、2个 D、1个二、填空题
-
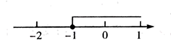
11. 命题“对应角相等的三角形是全等三角形”是命题（填“真”或者“假”）.12. 在直角三角形中，两条直角边的长分别是8和15，则斜边上的中线长是.13. 已知关于 的不等式 的解在数轴上的表示如图，则 的值是.
14. 如图所示，“赵爽弦图”是由8个全等的直角三角形拼接而成的，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为 ，已知 ，则 的值是.
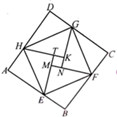15. 在△ABC中，AC=AB=5，一边上的高为3，则底边BC的长是.16. 如图钢架中，∠A= 度，焊上等长的钢条 ...来加固钢架，若 ，这样的钢条至多需要6根，那么 的取值范围是.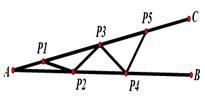
三、解答题
-
17. 解不等式： ，并把解表示在数轴上。18. 如图所示，点E，F在AC上，AB∥CD，AB=CD，AE=CF，求证△ABF≌△CDE.
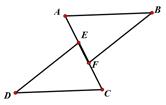19. 在Rt△ABC中，∠ACB=90°，利用直尺和圆规作图
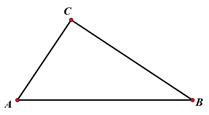(1)、作出AB边上的中线CD；(2)、作出△ABC的角平分线AE；(3)、若AC=5，BC=12，求出斜边AB上的高的长度.20. 已知：如图，在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG⊥CE于G，且CD=AE.
(1)、求证：CG=EG.(2)、求证：∠B=2∠ECB．21. BD、CE分别是△ABC的边AC、AB上的高，P在BD的延长线上，且BP=AC，点Q在CE上，CQ=AB．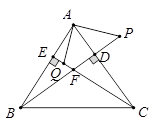
求证：
(1)、AP=AQ ；(2)、AP⊥AQ．22. 随着人们生活质量的提高，净水器已经慢慢走入了普通百姓家庭，某电器公司销售每台进价分别为 2000 元，1700 元的A，B两种型号的净水器，下表是近两周的销售情况：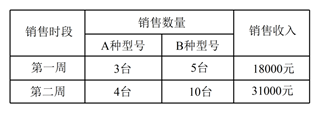
(1)、求A，B两种型号的净水器的销售单价；(2)、若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台，求 A种型号的净水器最多能采购多少台?(3)、在（2）的条件下，公司销售完这 30 台净水器能否实现利润超过12800 元的目标?若能，请给出相应的采购方案；若不能，请说明理由．23. 如图，已知在Rt△ABC中，∠ACB=90°，AC=8 ， BC=16，D是AC上的一点，CD=3，点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连结AP.
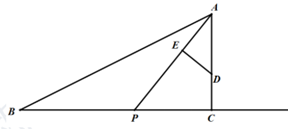(1)、当t=3秒时，求AP的长度(结果保留根号)；(2)、当△ABP为等腰三角形时，求t的值；(3)、过点D做DE⊥AP于点E.在点P的运动过程中，当t为何值时，能使DE=CD？