浙教版2019-2020学年初中数学八年级上学期期末复习专题11 一次函数
试卷更新日期:2019-12-17 类型:复习试卷
一、单选题
-
1. 下列说法正确的是( )A、常量是指永远不变的量 B、具体的数一定是常量 C、字母一定表示变量 D、球的体积公式V= πr³,变量是π,r2. 下列函数中,一定是一次函数的是
 A、
A、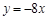 B、
B、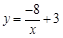 C、
C、 D、
D、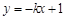 3. 已知函数 是正比例函数,则m的值是( )A、2 B、﹣2 C、±2 D、4. 大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为 ,水位高度变量为 ,下列图象中最符合故事情景的大致图象是( )
3. 已知函数 是正比例函数,则m的值是( )A、2 B、﹣2 C、±2 D、4. 大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为 ,水位高度变量为 ,下列图象中最符合故事情景的大致图象是( ) A、
A、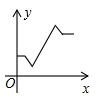 B、
B、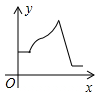 C、
C、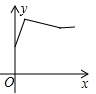 D、
D、 5. 点A(1,y1)、B(2,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不确定6. 若正比例函数y=kx的图象过点(-2,1),则一次函数y=kx-k的图象过( )A、第一、二、四象限 B、第一、三、四象限 C、第二、三、四象限 D、第一、二、三象限7. 表示一次函数y=mx+n与正比例函数y=mnx(m、n是常数且mn≠0)图象是( )A、
5. 点A(1,y1)、B(2,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不确定6. 若正比例函数y=kx的图象过点(-2,1),则一次函数y=kx-k的图象过( )A、第一、二、四象限 B、第一、三、四象限 C、第二、三、四象限 D、第一、二、三象限7. 表示一次函数y=mx+n与正比例函数y=mnx(m、n是常数且mn≠0)图象是( )A、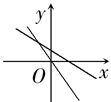 B、
B、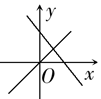 C、
C、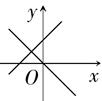 D、
D、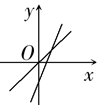 8. 一次函数y=kx+b(k≠0)的图象经过一二四象限,则k和b的取值范围是( )A、k>0,b>0 B、k<0,b>0 C、k>0,b<0 D、k<0,b<09. 若正比例函数 的图象经过点 和点 ,当 时, ,则 的取值范围是( )A、 B、 C、 D、10. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、
8. 一次函数y=kx+b(k≠0)的图象经过一二四象限,则k和b的取值范围是( )A、k>0,b>0 B、k<0,b>0 C、k>0,b<0 D、k<0,b<09. 若正比例函数 的图象经过点 和点 ,当 时, ,则 的取值范围是( )A、 B、 C、 D、10. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、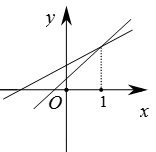 B、
B、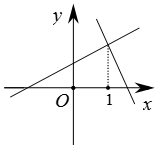 C、
C、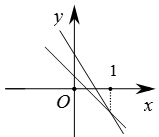 D、
D、
二、填空题
-
11. 函数 中,自变量 的取值范围是.12. 若函数y=(a-3)x|a|-2+2a+1是一次函数,则a=.13. 为节约用水,某市居民生活用水按级收费,具体收费标准如下表:
用水量(吨)
不超过17吨的部分
超过17吨不超过31吨的部分
超过31吨的部分
单位(元/吨)
3
5
7
设某户居民家的月用水量为 吨,应付水费为 元,则 关于 的函数表达式为.
14. 已知y是关于x的一次函数,下表列出了部分对应值,则m的值为.x
0
3
4
y
20
m
8
15. 点A(m,﹣3)向下平移3个单位后,恰好落在正比例函数y=﹣6x的图象上,则m的值为.16. 如图,在直角坐标系中,过点 分别向x轴,y轴作垂线,垂足分别为点B,C,取AC的中点P,连结OP,作点C关于直线OP的对称点D,直线PD与AB交于点Q,则线段PQ的长为 , 直线PQ的函数表达式为.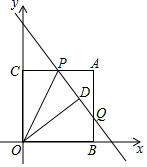
三、解答题
-
17. 已知函数 和 .
 (1)、在同一个平面直角坐标系中画出这两个函数的图象;(2)、根据图象,写出它们的交点坐标;18. 小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与动时间t(s)之间的关系如图2所示。
(1)、在同一个平面直角坐标系中画出这两个函数的图象;(2)、根据图象,写出它们的交点坐标;18. 小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与动时间t(s)之间的关系如图2所示。 (1)、根据函数的定义,请判断变量h是否为关于t的函数?(2)、结合图象回答:
(1)、根据函数的定义,请判断变量h是否为关于t的函数?(2)、结合图象回答:①当t=0.7s时,h的值是多少?并说明它的实际意义,
②秋千摆动第一个来回需多少时间?
19. 某农机租赁公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如下表:每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元
(1)、设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机天获得的租金为y元,求y关于x的函数关系式,并写出自变量的取值范围:(2)、若使农机租赁公司这50台收割机一天所获租金不低于79600元,为农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.20. 如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.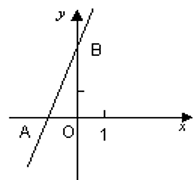 (1)、求A,B两点的坐标;(2)、过B点作直线BP与x轴相交于P,且使OP=2OA,求ΔABP的面积.21. 有一科技小组进行了机器人行走性能试验.在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,经过7min同时到达C点,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
(1)、求A,B两点的坐标;(2)、过B点作直线BP与x轴相交于P,且使OP=2OA,求ΔABP的面积.21. 有一科技小组进行了机器人行走性能试验.在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,经过7min同时到达C点,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题: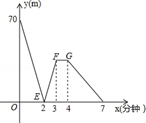 (1)、A、B两点之间的距离是.m,甲机器人前2min的速度为.m/min;(2)、若前3min甲机器人的速度不变,求线段EF所在直线的函数解析式;(3)、直接写出两机器人出发多长时间相距28m.22. 随着生活水平的逐步提高,某单位的私家小轿车越来越多,为确保有序停车,单位决定筹集资金维修和新建一批停车棚.该单位共有42辆小轿车,准备维修和新建的停车棚共有6个,费用和可供停车的辆数及用地情况如下表:
(1)、A、B两点之间的距离是.m,甲机器人前2min的速度为.m/min;(2)、若前3min甲机器人的速度不变,求线段EF所在直线的函数解析式;(3)、直接写出两机器人出发多长时间相距28m.22. 随着生活水平的逐步提高,某单位的私家小轿车越来越多,为确保有序停车,单位决定筹集资金维修和新建一批停车棚.该单位共有42辆小轿车,准备维修和新建的停车棚共有6个,费用和可供停车的辆数及用地情况如下表:停车棚
费用(万元/个)
可停车的辆数(辆/个)
占地面积(m2/个)
新建
4
8
100
维修
3
6
80
已知可支配使用土地面积为580m2 , 若新建停车棚 个,新建和维修的总费用为 万元.
(1)、求 与 之间的函数关系;(2)、满足要求的方案有几种?(3)、为确保工程顺利完成,单位最少需要出资多少万元.23. 如图,直线y= x+6与x轴、y轴分别相交于点E、F,点A的坐标为(-6,0),P(x,y)是直线y= x+6上一个动点.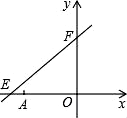 (1)、在点P运动过程中,试写出△OPA的面积s与x的函数关系式;(2)、当P运动到什么位置,△OPA的面积为 ,求出此时点P的坐标;(3)、过P作EF的垂线分别交x轴、y轴于C、D.是否存在这样的点P,使△COD≌△FOE?若存在,直接写出此时点P的坐标(不要求写解答过程);若不存在,请说明理由.24. 甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量 (个)与加工时间 (分)之间的函数关系,观察图象解决下列问题:
(1)、在点P运动过程中,试写出△OPA的面积s与x的函数关系式;(2)、当P运动到什么位置,△OPA的面积为 ,求出此时点P的坐标;(3)、过P作EF的垂线分别交x轴、y轴于C、D.是否存在这样的点P,使△COD≌△FOE?若存在,直接写出此时点P的坐标(不要求写解答过程);若不存在,请说明理由.24. 甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量 (个)与加工时间 (分)之间的函数关系,观察图象解决下列问题: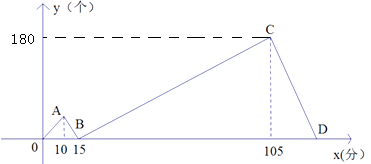 (1)、点B的坐标是 , B点表示的实际意义是;(2)、求线段BC对应的函数关系式和D点坐标;(3)、乙在加工的过程中,多少分钟时比甲少加工100个零件?(4)、为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
(1)、点B的坐标是 , B点表示的实际意义是;(2)、求线段BC对应的函数关系式和D点坐标;(3)、乙在加工的过程中,多少分钟时比甲少加工100个零件?(4)、为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.