浙教版2019-2020学年初中数学八年级上学期期末复习专题9 一元一次不等式(组)
试卷更新日期:2019-12-17 类型:复习试卷
一、单选题
-
1. 下列各式,是一元一次不等式的有( )
① > ② < ③ ④ ⑤
A、4个 B、3个 C、2个 D、1个2. 下列属于一元一次不等式组的是( )A、 B、 C、 D、3. 已知a<b,下列不等式中正确的是( )A、 B、 a﹣3< b﹣3 C、a+3>b+3 D、﹣3a<﹣3b4. 将不等式组 的解集表示在数轴上,下列表示正确的是( )A、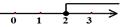 B、
B、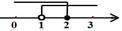 C、
C、 D、
D、 5. 如图,数轴上所示不等式组的解集是( ).
5. 如图,数轴上所示不等式组的解集是( ). A、x<-1或x≥3 B、x≤-1或x>3 C、-1≤x<3 D、-1<x≤36. 若m>n,则下列不等式变形错误的是( )A、m﹣5>n﹣5 B、﹣6m>﹣6n C、3m>3n D、7. 不等式3(x-2)≥x+4的解集是( )A、x≥5 B、x≥3 C、x≤5 D、x≥-58. 小明用100元钱去购买笔记本和钢笔共30件,已知每本笔记本3元,每支钢笔5元,求小明最多能买几支钢笔.设小明买了x支钢笔,依题意可列不等式为( )A、3x+5(30﹣x)≤100 B、3(30﹣x)+5≤100 C、5(30﹣x)≤100+3x D、5x≤100﹣3(30+x)9. 按如图的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否大于365”为一次操作.如果必须进行3次操作才能得到输出值,那么输入值x必须满足( )
A、x<-1或x≥3 B、x≤-1或x>3 C、-1≤x<3 D、-1<x≤36. 若m>n,则下列不等式变形错误的是( )A、m﹣5>n﹣5 B、﹣6m>﹣6n C、3m>3n D、7. 不等式3(x-2)≥x+4的解集是( )A、x≥5 B、x≥3 C、x≤5 D、x≥-58. 小明用100元钱去购买笔记本和钢笔共30件,已知每本笔记本3元,每支钢笔5元,求小明最多能买几支钢笔.设小明买了x支钢笔,依题意可列不等式为( )A、3x+5(30﹣x)≤100 B、3(30﹣x)+5≤100 C、5(30﹣x)≤100+3x D、5x≤100﹣3(30+x)9. 按如图的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否大于365”为一次操作.如果必须进行3次操作才能得到输出值,那么输入值x必须满足( ) A、x<50 B、x<95 C、50<x<95 D、50<x≤9510. 某商场促销,小鱼将促销信息告诉了妈妈,假设某一商品的定价为 ,并列出不等式为 ,那么小鱼告诉妈妈的信息是( )
A、x<50 B、x<95 C、50<x<95 D、50<x≤9510. 某商场促销,小鱼将促销信息告诉了妈妈,假设某一商品的定价为 ,并列出不等式为 ,那么小鱼告诉妈妈的信息是( )
A、买两件等值的商品可减100元,再打三折,最后不到1000元 B、买两件等值的商品可打三折,再减100元,最后不到1000元 C、买两件等值的商品可减100元,再打七折,最后不到1000元 D、买两件等值的商品可打七折,再减100元,最后不到1000元二、填空题
-
11. 不等式组 有4个整数解,则m的取值范围是 .12. 不等号填空:若a>b>0则 ; ; .13. 已知不等式组 的解集为 ,则 的值是.14. 已知关于x的不等式组 有解,则m的取值范围是。15. 一个长方形,两边长分别为xcm和10cm,如果它的周长小于80cm,面积大于100cm2 , 则x的取值范围是 cm.16. 对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n﹣ ≤x<n+ ,则(x)=n.如(0.46)=0,(3.67)=4.
给出下列关于(x)的结论:
①(1.493)=1;②(2x)=2(x);③若( )=4,则实数x的取值范围是9≤x<11;④当x≥0,m为非负整数时,有(m+2013x)=m+(2013x);⑤(x+y)=(x)+(y);其中,正确的结论有(填写所有正确的序号).
三、计算题
-
17. 解下列不等式,并把解集在数轴上表示出来(1)、2-5x≥8-2x(2)、18. 解下列不等式(组):(1)、 <(2)、19. 解不等式组 ,把解集在所给数轴上表示出来,并写出其整数解。
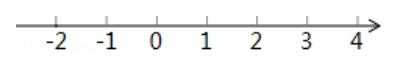 20. 某公司计划生产甲、乙两种产品共20件,其总产值w(万元)满足:1150<w<1200,相关数据如下表,为此,公司应怎样设计这两种产品的生产方案?
20. 某公司计划生产甲、乙两种产品共20件,其总产值w(万元)满足:1150<w<1200,相关数据如下表,为此,公司应怎样设计这两种产品的生产方案?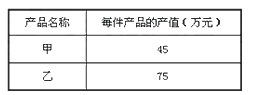 21. 某校艺术节时欲购40盆花卉布置舞台.现有甲、乙两种花卉可供选择,已知甲种花卉的单价为18元/盆,乙种花卉的单价为25元/盆.若学校计划用于购买花卉的费用最多为860元,且购买乙花卉不少于18盆.请你为该校设计购买方案,并求出最小的费用是多少元?22. 我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变,不等式组是否也具有类似的性质呢?请解答下列问题(1)、完成下列填空:
21. 某校艺术节时欲购40盆花卉布置舞台.现有甲、乙两种花卉可供选择,已知甲种花卉的单价为18元/盆,乙种花卉的单价为25元/盆.若学校计划用于购买花卉的费用最多为860元,且购买乙花卉不少于18盆.请你为该校设计购买方案,并求出最小的费用是多少元?22. 我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变,不等式组是否也具有类似的性质呢?请解答下列问题(1)、完成下列填空:已知
用“<”或“>”填空
4+23+1
﹣3﹣22﹣1
(2)、一般地,如果 那么a+cb+d(用“<”或“>”填空)请你利用不等式的基本性质说明上述不等式的正确性.23. 某小区积极创建环保示范社区,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知温馨提示牌的单价为每个30元,垃圾箱的单价为每个90元,共需购买温馨提示牌和垃圾箱共100个.(1)、若规定温馨提示牌和垃圾箱的个数之比为1:4,求所需的购买费用;(2)、若该小区至多安放48个温馨提示牌,且费用不超过6300元,请列举所有购买方案,并说明理由.24. 某公交公司有A,B型两种客车,它们的载客量和租金如下表:A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
学校根据实际情况,计划租用A、B型客车共5辆,同时送八年级师生到素质基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)、用含x的式子填写下表:车辆数(辆)
载客量
租金(元)
A
x
45x
400x
B
5-x
(2)、若要保证租车费用不超过1900元,求最多租用A型客车多少辆?(3)、在(2)的条件下,若八年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案。