浙教版2019-2020学年初中数学八年级上学期期末复习专题8 勾股定理
试卷更新日期:2019-12-17 类型:复习试卷
一、单选题
-
1. 直角三角形的两条边长为5和12,它的斜边长为( )A、13 B、 C、13或 D、13或122. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
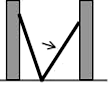 A、2.2米 B、2.3米 C、2.4米 D、2.5米3. 我国是最早了解勾股定理的国家之一 下面四幅图中,不能证明勾股定理的是A、
A、2.2米 B、2.3米 C、2.4米 D、2.5米3. 我国是最早了解勾股定理的国家之一 下面四幅图中,不能证明勾股定理的是A、 B、
B、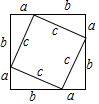 C、
C、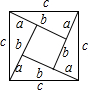 D、
D、 4. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为( )
4. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为( )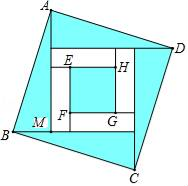 A、14S B、13S C、12S D、11S5. 三角形的三边a,b,c满足(a+b)2-c2=2ab,则此三角形是( ).A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形6. 以a.b.c为边的三角形是直角三角的为( )A、a=2,b=3,c=4 B、a=1,b= ,c=2 C、a=4,b=5,c=6 D、a=2,b=2,c=7. 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( ).
A、14S B、13S C、12S D、11S5. 三角形的三边a,b,c满足(a+b)2-c2=2ab,则此三角形是( ).A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形6. 以a.b.c为边的三角形是直角三角的为( )A、a=2,b=3,c=4 B、a=1,b= ,c=2 C、a=4,b=5,c=6 D、a=2,b=2,c=7. 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( ).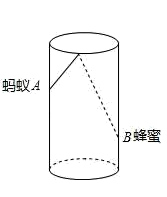 A、13cm B、 cm C、2 cm D、20cm8. 如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )
A、13cm B、 cm C、2 cm D、20cm8. 如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )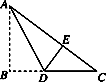 A、6 B、5 C、4 D、39. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A、6 B、5 C、4 D、39. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )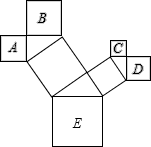 A、13 B、26 C、34 D、4710. 如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为 , , ,则 , , 之间的关系是( )
A、13 B、26 C、34 D、4710. 如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为 , , ,则 , , 之间的关系是( )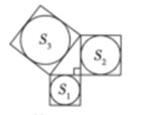 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定二、填空题
-
11. 写四组勾股数组. , , , .
12. 如图,两个正方形的面积分别是289和225,则字母A所代表的正方形的边长为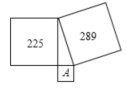 13. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为 ,此时正方形EFGH的面积为5.问:当格点弦图中的正方形ABCD的边长为 时,正方形EFGH的面积的所有可能值是(不包括5).
13. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为 ,此时正方形EFGH的面积为5.问:当格点弦图中的正方形ABCD的边长为 时,正方形EFGH的面积的所有可能值是(不包括5).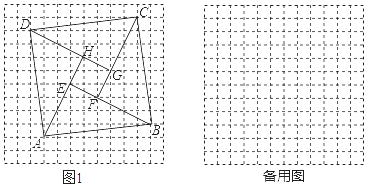 14. 如图是一个长8m,宽6m,高2m的有盖仓库,在其内壁的A处 长的四等分 有一只壁虎,B处 宽的三等分 有一只蚊子,则壁虎爬到蚊子处最短距离为
14. 如图是一个长8m,宽6m,高2m的有盖仓库,在其内壁的A处 长的四等分 有一只壁虎,B处 宽的三等分 有一只蚊子,则壁虎爬到蚊子处最短距离为 15. 如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯至少要米长.
15. 如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯至少要米长. 16. 《九章算术》是我国古代重要的数学著作之一,在“勾股”中记载了一道“折竹抵地”问题:“今有竹高一丈,未折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程求出AC的长为.
16. 《九章算术》是我国古代重要的数学著作之一,在“勾股”中记载了一道“折竹抵地”问题:“今有竹高一丈,未折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程求出AC的长为.
三、解答题
-
17. 如图,某校A与公路距离为3千米,又与该公路旁上的某车站D的距离为5千米,现要在公路边建一个商店C,使之与该校A及车站D的距离相等,则商店与车站的距离约为多少?
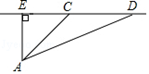 18. 如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,你能找到几个这样的C点?把它们都画出来。
18. 如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,你能找到几个这样的C点?把它们都画出来。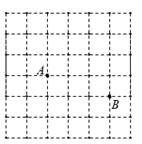 19. 如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
19. 如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?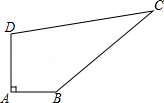 20. 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明灵感,他惊喜地发现,当四个全等的直角三角形如图摆放时,可以用“面积法"来证明 .请你写出证明过程.
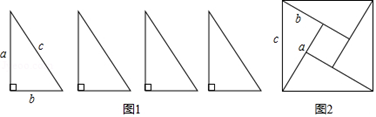
20. 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明灵感,他惊喜地发现,当四个全等的直角三角形如图摆放时,可以用“面积法"来证明 .请你写出证明过程. 21. △ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2 , 若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
21. △ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2 , 若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.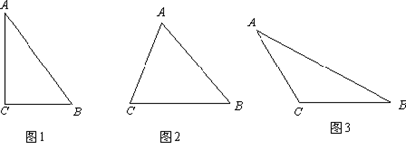 22. 中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC 中,∠ACB=90°,若 AC=b,BC=a,请你利用这个图形解决下列问题:
22. 中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC 中,∠ACB=90°,若 AC=b,BC=a,请你利用这个图形解决下列问题: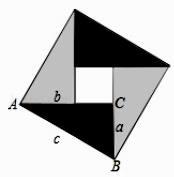 (1)、试说明 a2+b2=c2;(2)、如果大正方形的面积是 10,小正方形的面积是2,求(a+b)2的值.
(1)、试说明 a2+b2=c2;(2)、如果大正方形的面积是 10,小正方形的面积是2,求(a+b)2的值.