浙教版2019-2020学年初中数学八年级上学期期末复习专题7 直角三角形
试卷更新日期:2019-12-17 类型:复习试卷
一、单选题
-
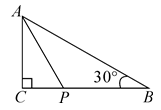
1. 在一个直角三角形中,有一个锐角等于 ,则另一个锐角的度数是( )A、 B、 C、 D、2. 以下列各组数为三边的三角形中不是直角三角形的是( )A、25、7、24 B、41、40、9 C、6、5、4 D、9、12、153. 下列命题:①有一个角为60°的等腰三角形是等边三角形;②三边长为 , , 的三角形为直角三角形;③等腰三角形的两条边长为2, 4,则等腰三角形的周长为10或8;④在直角三角形中,30°角所对直角边等于斜边的一半。正确的个数有( )A、4个 B、3个 C、2个 D、1个4. 如图,在Rt△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP的长不可能是( )
 A、3.5 B、4.2 C、5. 8 D、75. 直角三角形的斜边长为4,则它的斜边上的中线长为( )A、2 B、4 C、8 D、166. 如图,△ABC中,BC=18,若BD⊥AC于D点,CE⊥AB于E点,F,G分别为BC、DE的中点,若ED=10,则FG的长为( )
A、3.5 B、4.2 C、5. 8 D、75. 直角三角形的斜边长为4,则它的斜边上的中线长为( )A、2 B、4 C、8 D、166. 如图,△ABC中,BC=18,若BD⊥AC于D点,CE⊥AB于E点,F,G分别为BC、DE的中点,若ED=10,则FG的长为( )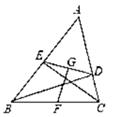 A、 B、 C、8 D、97. 下面说法不正确的是( )A、有一角和一边对应相等的两个直角三角形全等 B、有两边对应相等的两个直角三角形全等 C、有两角对应相等的两个直角三角形全等 D、有两角和一边对应相等的两个直角三角形全等8. 如图,P是∠AOB的平分线OC上一点(不与O重合),过P分别向角的两边作垂线PD,PE,垂足是D,E,连结DE,那么图中全等的直角三角形共有( )
A、 B、 C、8 D、97. 下面说法不正确的是( )A、有一角和一边对应相等的两个直角三角形全等 B、有两边对应相等的两个直角三角形全等 C、有两角对应相等的两个直角三角形全等 D、有两角和一边对应相等的两个直角三角形全等8. 如图,P是∠AOB的平分线OC上一点(不与O重合),过P分别向角的两边作垂线PD,PE,垂足是D,E,连结DE,那么图中全等的直角三角形共有( )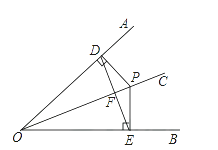 A、3对 B、2对 C、1对 D、没有9. 如图,已知AB=AD,添加一个条件后,仍然不能判定△ABC≌△ADC的是( )
A、3对 B、2对 C、1对 D、没有9. 如图,已知AB=AD,添加一个条件后,仍然不能判定△ABC≌△ADC的是( )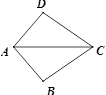 A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°10. 如图,已知在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连结EF.当△BEF是直角三角形时,t的值为( ).
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°10. 如图,已知在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连结EF.当△BEF是直角三角形时,t的值为( ).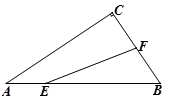 A、 B、1 C、 或1或 D、 或1或
A、 B、1 C、 或1或 D、 或1或二、填空题
-
11. 如图,AE是 的角平分线, 于点D , 若 , , 度
 12. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .13. 如图,∠ABC=∠ADC=90°,∠ACB=30°,∠DAC=45°,E是AC的中点,连结BE,DE,BD,F是BD的中点.则∠BEF=.
12. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .13. 如图,∠ABC=∠ADC=90°,∠ACB=30°,∠DAC=45°,E是AC的中点,连结BE,DE,BD,F是BD的中点.则∠BEF=. 14. 如图,∠AOB=50°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=.
14. 如图,∠AOB=50°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=. 15. 若直角三角形斜边上的高和中线分别是 5 cm 和 6 cm,则面积为 ,16. 如图,OP平分∠AOB,PD⊥OB于D,∠OPD=60°,PO=4,则点P到边OA的距离是.
15. 若直角三角形斜边上的高和中线分别是 5 cm 和 6 cm,则面积为 ,16. 如图,OP平分∠AOB,PD⊥OB于D,∠OPD=60°,PO=4,则点P到边OA的距离是.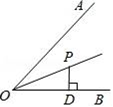
三、解答题
-
17. 如图,在△ABC中,∠ACB=90°,CD是高.
 (1)、图中有几个直角三角形?是哪几个?(2)、∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
(1)、图中有几个直角三角形?是哪几个?(2)、∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
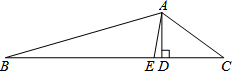
18. 如图,在△ABC中,∠B=∠C=60°,AD⊥BC于D,E为AC的中点,CB=8,求DE的长. 19. 已知:如图,AB⊥BD于点B,CD⊥BD于点D.P是BD上一点,且AP=PC,AB=PD,求证:AP⊥CP.
19. 已知:如图,AB⊥BD于点B,CD⊥BD于点D.P是BD上一点,且AP=PC,AB=PD,求证:AP⊥CP.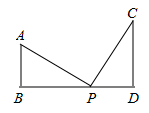 20. 如图,将△ABC 分别沿 AB,AC 翻折得到△ABD 和△AEC,线段 BD 与AE 交于点 F.
20. 如图,将△ABC 分别沿 AB,AC 翻折得到△ABD 和△AEC,线段 BD 与AE 交于点 F.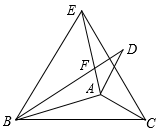 (1)、若∠ABC=16º,∠ACB=30°,求∠DAE 及∠BFE 的值;(2)、若 BD 与 CE 所在的直线互相垂直,求∠CAB 的度数.21. 如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)、若∠ABC=16º,∠ACB=30°,求∠DAE 及∠BFE 的值;(2)、若 BD 与 CE 所在的直线互相垂直,求∠CAB 的度数.21. 如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P. (1)、若∠B=40°,∠AEC=75°,求证:AB=BC;(2)、若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.22. 如图,已知 平分 , 于 , 于 ,且 .
(1)、若∠B=40°,∠AEC=75°,求证:AB=BC;(2)、若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.22. 如图,已知 平分 , 于 , 于 ,且 . (1)、求证: ≌ .(2)、若 , , ,求 的长.23. 已知:如图,在△ABC中,AD是BC边上的高,∠C=30°,∠ABC=45°,BE是AC边上的中线.
(1)、求证: ≌ .(2)、若 , , ,求 的长.23. 已知:如图,在△ABC中,AD是BC边上的高,∠C=30°,∠ABC=45°,BE是AC边上的中线.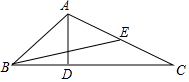 (1)、求证:AC=2BD;(2)、求∠CBE的度数;(3)、若点E到边BC的距离为 ,求BC的长.24. 阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,
(1)、求证:AC=2BD;(2)、求∠CBE的度数;(3)、若点E到边BC的距离为 ,求BC的长.24. 阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
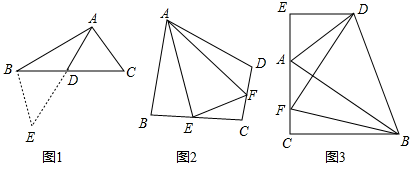 (1)、如图1,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
(1)、如图1,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是;
(2)、问题解决:如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,边CD上的两点,且∠EAF= ∠BAD,求证:BE+DF=EF.
(3)、问题拓展:如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC外角平分线上一点,DE⊥AC交CA延长线于点E,F是AC上一点,且DF=DB.求证:AC-AE= AF.