浙教版2019-2020学年初中数学八年级上学期期末复习专题6 等腰三角形和等边三角形
试卷更新日期：2019-12-17 类型：复习试卷
一、单选题
-
1. 如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是（ ）
A、AD⊥BC B、AD平分∠BAC C、AB＝2BD D、∠B＝∠C2. 一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是（ ）A、13cm B、14cm C、13cm或14cm D、以上都不对3. 如图△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D交AC于点E，那么下列结论中正确的是（ ）
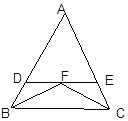
①△BDF和△CEF都是等腰三角形
②DE=BD+CE
③△ADE的周长等于AB和AC的和
④BF=CF
A、①②③④ B、①②③ C、①② D、①4. 如图，AD＝BC＝BA，那么∠1与∠2之间的关系是（ ）
A、∠1＝2∠2 B、2∠1+∠2＝180° C、∠1+3∠2＝180° D、3∠1﹣∠2＝180°5. 如图，在△ABC中，∠C=29°，D为边AC上一点，且AB=AD，DB=DC，则∠A的度数为（ ）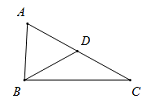
A、54° B、58° C、61° D、64°6. 如图，已知△ABC中，AB=3，AC=5，BC=7，在△ABC所在平面内一条直线，将△ABC分割成两个三角形，使其中有一个边长为3的等腰三角形，则这样的直线最多可画（ ）
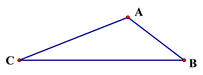A、5条 B、4条 C、3条 D、2条7. 如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）
A、1 B、1.5 C、2 D、48. 下列命题：①有一个角为60°的等腰三角形是等边三角形；②三边长为 ， ， 的三角形为直角三角形；③等腰三角形的两条边长为2， 4，则等腰三角形的周长为10或8；④在直角三角形中，30°角所对直角边等于斜边的一半。正确的个数有（ ）A、4个 B、3个 C、2个 D、1个9. △ABC中，AB=AC，CD为AB上的高，且△ADC为等腰三角形，则∠BCD等于（ ）A、67.5° B、22.5° C、45° D、67.5°或22.5°10. 如图所示，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，OC．以下五个结论：①△ACD≌△BCE；②△AOC≌△BQC ； ③△APC≌△BOC； ④△DPC≌△EQC；⑤ ∠AOB＝60°．其中正确的是（ ）
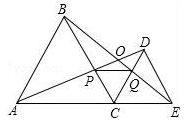A、①②③④⑤ B、①④⑤ C、①④ D、①③④二、填空题
-
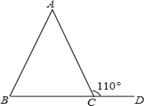
11. 已知等腰三角形的两边长分别为3和5，则它的周长是 ．12. 等腰三角形的一腰上的高与另一腰所在直线的夹角为40°，则这个三角形的底角为 ．13. 如图，在△ABC中，AB=AC，外角∠ACD=110°，则∠A=.
14. 如图在△ABC中，BF、CF是角平分线，DE∥BC，分别交AB、AC于点D、E，DE经过点F．结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE； ③△ADE的周长=AB+AC；④BF=CF．其中正确的是（填序号）
15. 在△ABC中，∠C=90°，AC=8cm．BC=6 cm， 动点P从点C开始，按C→A→B→C的路径绕△ABC的边运动一周，速度为每秒2cm，运动的时间为t秒．则△BCP为等腰三角形时t的值是 ．16. 如图，已知△ABC为等边三角形，高AH＝10 cm，P为AH上的一个动点，D为AB的中点，则PD＋PB的最小值为cm.
三、解答题
-
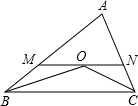
17. 如图，△ABC中，∠ABC、∠ACB的平分线相交于O，MN过点O且与BC平行.△ABC的周长为20，△AMN的周长为12，求BC的长.
18. 如图，已知△ABC是正三角形，D，E，F分别是各边上的一点，且AD=BE=CF.请你说明△DEF是正三角形.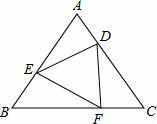
19. 将一个边长为5、12、13的直角三角形拼上一个三角形后可以拼成一个等腰三角形，图1就是其中的一种拼法，请你画出其他所有可能的情形，并在图上标出所拼成等腰三角形的腰的长度．（选用图2中的备用图画图，每种情形用一个图形单独表示，并用①、②、③…编号，若备用图不够，请自己画图补充）
20. 如图，在△ABC 中，AB=AC，CD是∠ACB的平分线，DE∥BC，交AC于点 E.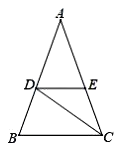
(1)、求证：DE=CE.(2)、若∠CDE=25°，求∠A 的度数.21. 如图，已知△ABC是等边三角形，BD是AC上的高线.作AE⊥AB于点A，交BD的延长线于点E.取BE的中点M，连结AM.
(1)、求证：△AEM是等边三角形；(2)、若AE=2，求△AEM的面积.22. 如图所示，边长为2的等边三角形ABC中，D点在边BC上运动(不与B、C重合)，点E在边AB的延长线上，点F在边AC的延长线上，AD=DE=DF.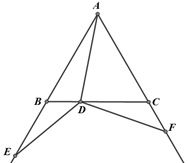
(1)、若∠AED=30°，则∠ADB=°.(2)、求证：△BED≌△CDF(3)、点D在BC边上从B至C的运动过程中，△BED周长变化规律为（ ）A、不变 B、一直变小 C、先变大后变小 D、先变小后变大23. 在等腰Rt△ABC中，∠BAC=90°，AB=AC，在△ABC外作∠ACM= ∠ABC，点D为直线BC上的动点，过点D作直线CM的垂线，垂足为E，交直线AC于F.
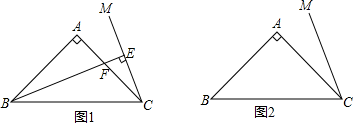(1)、①当点D在线段BC上时，如图1所示，求∠EDC的度数②探究线段DF与EC的数量关系，并证明；
(2)、当点D运动到CB延长线上时，请你画出图形，并证明此时DF与EC的数量关系.24. 数学课上，张老师举了下面的例题：例1：等腰△ABC中，∠A=100°，求∠B的度数．(答案：40°)
例2：等腰△ABC中，∠A=50°，求∠B的度数．(答案：50°或65°或80°)
张老师启发同学们进行变式，小敏编了如下一题：
变式：等腰△ABC中，∠A=70°，求∠B的度数．
(1)、请你解答小敏编的变式题：(2)、解第(1)小题后小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同．如果在等腰△ABC中，设∠A=x°，当∠B有三个不同的度数时，请你探索x的取值范围．