浙教版2019-2020学年初中数学八年级上学期期末复习专题5 轴对称
试卷更新日期：2019-12-17 类型：复习试卷
一、单选题
-
1. 下列“微信表情”中属于轴对称图形的是（ ）A、
B、 
C、
D、
2. 下列剪纸作品中，是轴对称图形的为（ ）A、
B、
C、
D、
3. 小明从镜子中看到对面电子钟示数如图所示，这时的时刻应是（ ）
A、21∶10 B、10∶21 C、10∶51 D、12∶014. 如图，是一个三角板，则下列选项中可能是由该图经过一次轴对称变换后得到的是（ ）
A、
B、
C、
D、
5. 在直角坐标系xOy中，△ABC关于直线y=1轴对称，已知点A坐标是（4，4），则点B的坐标是（ ）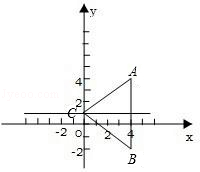
A、（4，﹣4） B、（﹣4，2） C、（4，﹣2） D、（﹣2，4）6. 如图，∠MON内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，GH分别交OM、ON于A，B点，若∠MON=35°，则∠GOH=（ ）
A、60° B、70° C、55° D、90°7. 如图是一个6×6的正方形网格，每个小正方形的顶点都是格点，Rt△ABC的顶点都在图中的格点上，其中点A、点B的位置如图所示，则点C可能的位置共有（ ）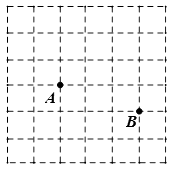
A、9个 B、8个 C、7个 D、6个8. 在平面直角坐标系中，已知 、 ，若要在x轴上找一点P，使 最短，则点P的坐标为（ ）A、 B、 C、 D、9. 如图，直线L是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站，向P，Q 两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（ ）A、
B、
C、
D、
10. 如果P点的坐标为（a，b），它关于y轴的对称点为P1 ， P1关于x轴的对称点为P2 ， 已知P2的坐标为（﹣2，3），则点P的坐标为（ ）A、（﹣2，﹣3） B、（2，﹣3） C、（﹣2，3） D、（2，3）二、填空题
-
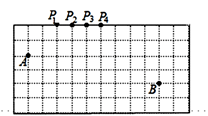
11. 如图，在一个规格为6×12（即6×12个小正方形）的球台上，有两个小球A，B.若击打小球A，经过球台边的反弹后，恰好击中小球B，那么小球A击出时，应瞄准球台边上的点.（填P1至P4点中的一个）.
12. 如果△ABC与△A'B'C'关于直线l对称，且∠A＝50°，∠B'＝70°，那么∠C'＝.13. 如图，P为△ABC内的一点，D，E，F分别是点P关于边AB，BC，CA所在直线的对称点，那么∠ADB+∠BEC+∠CFA=°.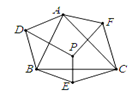
14. 如图，在△ABC中，AB=10cm，AC=6cm，BC=8cm，点D、E分别在AB、AC上，且△BCD和△BED关于BD对称，则△ADE的周长为cm．
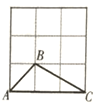
15. 如图，∠AOB＝30º，∠AOB内有一定点P，且OP＝10.在OA上有一动点Q，OB上有一动点R.若ΔPQR周长最小，则最小周长是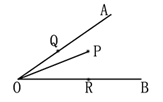
16. 如图，在3×3的正方形网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形．图中的△ABC为格点三角形，在图中最多能画出个格点三角形与△ABC成轴对称．
三、解答题
-
17. 如图，在 的正方形网格中，有格点 和 ，且 和 关于某条直线成轴对称，请在下面给出的图中，画出3个不同位置的 及其对称轴MN.
18. 如图，四边形ABCD中，∠BAD=100°，∠BCD=70°，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，求∠B的度数.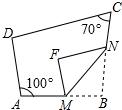
19. 如图，点P是∠AOB内一点，分别作出P点关于OA、OB的对称点E、F，连接EF交OA于M，交OB于N，EF=15，求△PMN的周长．
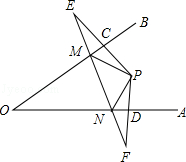20. 如果△ABC关于x轴进行轴对称变换后，得到△A1B1C1 ， 而△A1B1C1关于y轴进行轴对称变换后，得到△A2B2C2 ， 若△ABC三个顶点坐标分别为A（-2，3）、B（-4，2）、C（-1，0），请你分别写出△A1B1C1与△A2B2C2各顶点坐标．
21. 下面两图均是4×4的正方形网格，格点A，格点B和直线l的位置如图所示，点P在直线l上.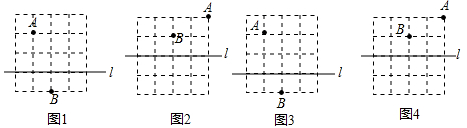
(1)、请分别在图1和图2中作出点P，使PA+PB最短；(2)、请分别在图3和图4中作出点P，使PA-PB最长.22. 如图，△ABC的三个顶点分别是A(-4，1)，B(-2，1)，C(-1，3)．以x轴为对称轴，将△ABC作轴对称变换得到△A1B1C1；然后将△A1B1C1向右平移6个单位后得到△A2B2C2 ．
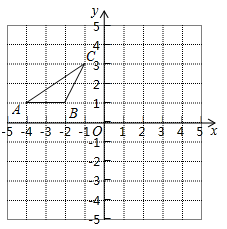(1)、请在图中作出△A1B1C1；(2)、直接写出经过上述两次变换后，对应点A2的坐标．23. 如图，在长度为1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上．
(1)、在图中画出与△ABC关于直线l成轴对称的△AB′C′；(2)、三角形ABC的面积为；(3)、以AC为边作与△ABC全等的三角形，则可作出个三角形与△ABC全等；(4)、在直线l上找一点P，使PB+PC的长最短．24. 已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C、D的坐标分别为A（9，0）、C（0，4），D（5，0），点P从点O出发，以每秒1个单位长度的速度沿O
C B A运动，点P的运动时间为t秒. 
(1)、当t=2时，求直线PD的解析式。(2)、当P在BC上，OP+PD有最小值时，求点P的坐标。(3)、当t为何值时，△ODP是腰长为5的等腰三角形？（直接写出t的值）.