浙教版2019-2020学年初中数学八年级上学期期末复习专题3 全等三角形的性质、判定与应用
试卷更新日期:2019-12-17 类型:复习试卷
一、单选题
-
1. 下列图形是全等图形的是( )A、
 B、
B、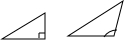 C、
C、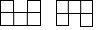 D、
D、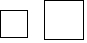 2. 下列选项中表示两个全等的图形的是( )A、形状相同的两个图形 B、周长相等的两个图形 C、面积相等的两个图形 D、能够完全重合的两个图形3. 下列不是利用三角形的稳定性的是( )A、伸缩晾衣架 B、三角形房架 C、自行车的三角形车架 D、矩形门框的斜拉条4. 如右图,△ABC≌△CDA,AB=4,BC=5,AC=6,则AD的长为( )
2. 下列选项中表示两个全等的图形的是( )A、形状相同的两个图形 B、周长相等的两个图形 C、面积相等的两个图形 D、能够完全重合的两个图形3. 下列不是利用三角形的稳定性的是( )A、伸缩晾衣架 B、三角形房架 C、自行车的三角形车架 D、矩形门框的斜拉条4. 如右图,△ABC≌△CDA,AB=4,BC=5,AC=6,则AD的长为( )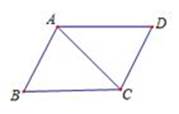 A、4 B、5 C、6 D、不能确定5. 如图,用尺规作图作已知角平分线,其根据是构造两个三形全等,它所用到的判别方法是( )
A、4 B、5 C、6 D、不能确定5. 如图,用尺规作图作已知角平分线,其根据是构造两个三形全等,它所用到的判别方法是( )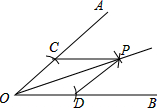 A、SAS B、AAS C、ASA D、SSS6. 某实验室有一块三角形玻璃,被摔成如图所示的四块,胡老师想去店里买一块形状、大小与原来一样的玻璃,胡老师要带的玻璃编号是( )
A、SAS B、AAS C、ASA D、SSS6. 某实验室有一块三角形玻璃,被摔成如图所示的四块,胡老师想去店里买一块形状、大小与原来一样的玻璃,胡老师要带的玻璃编号是( )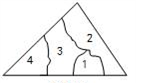 A、1 B、2 C、3 D、47. 在下列条件中,不能说明△ABC≌△A′B′C'的是( )A、∠A=∠A′,∠C=∠C′,AC=A'C' B、∠B=∠B′,∠C=∠C′,AB=A′B' C、∠A=∠A′,AB=A′B′,BC=B'C' D、AB=A′B′,BC=B'C,AC=A′C'8. 如图中,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若点E,B,D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积S是( )
A、1 B、2 C、3 D、47. 在下列条件中,不能说明△ABC≌△A′B′C'的是( )A、∠A=∠A′,∠C=∠C′,AC=A'C' B、∠B=∠B′,∠C=∠C′,AB=A′B' C、∠A=∠A′,AB=A′B′,BC=B'C' D、AB=A′B′,BC=B'C,AC=A′C'8. 如图中,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若点E,B,D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积S是( ) A、50 B、44 C、38 D、329. 如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A、50 B、44 C、38 D、329. 如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )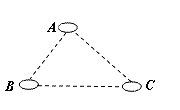 A、在AC,BC两边高线的交点处 B、在AC,BC两边中线的交点处 C、在AC,BC两边垂直平分线的交点处 D、在∠A,∠B内角平分线的交点处10. 如图,AD是∆ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7 ,DE=2,AB=4,则AC的长是( )
A、在AC,BC两边高线的交点处 B、在AC,BC两边中线的交点处 C、在AC,BC两边垂直平分线的交点处 D、在∠A,∠B内角平分线的交点处10. 如图,AD是∆ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7 ,DE=2,AB=4,则AC的长是( )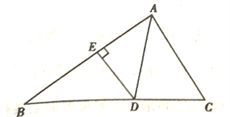 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
11. 如图,已知△ABC≌△DEC,∠E=40°,∠ACB=110°,则∠D的度数为 .
 12. 如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=cm.
12. 如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=cm.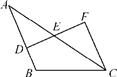 13. 如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于时,ΔABC和ΔPQA全等.
13. 如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于时,ΔABC和ΔPQA全等.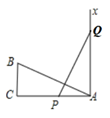 14. 如图,方格纸中△DEF的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则与△DEF全等的格点(顶点在每个小格的顶点上)三角形能画个.
14. 如图,方格纸中△DEF的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则与△DEF全等的格点(顶点在每个小格的顶点上)三角形能画个.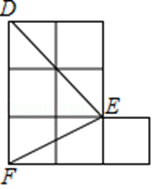 15. 如图,△ABC中∠ABC=∠ACB,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC=
15. 如图,△ABC中∠ABC=∠ACB,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC=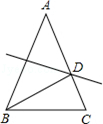 16. 如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=15,BD:CD=3:2,则点D到AB的距离是 .
16. 如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=15,BD:CD=3:2,则点D到AB的距离是 .
三、解答题
-
17. 如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
 (1)、在边BC上确定一点P,使得PA+PC=BC;(2)、作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
(1)、在边BC上确定一点P,使得PA+PC=BC;(2)、作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
18. 如图所示,已知点P是△ABC三条角平分线的交点,PD⊥AB , 若PD=5,△ABC的周长为20,求△ABC的面积.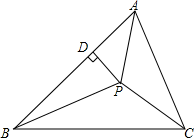 19. 已知,如图,在△ABC中,∠ACB=90°,AC=BC , 直线MN经过点C , 且AD⊥MN于点D , BE⊥MN于点E;试猜测线段DE、AD、BE之间的数量关系,并说明理由.
19. 已知,如图,在△ABC中,∠ACB=90°,AC=BC , 直线MN经过点C , 且AD⊥MN于点D , BE⊥MN于点E;试猜测线段DE、AD、BE之间的数量关系,并说明理由. 20. 如图,已知AB∥CF,DE=EF
20. 如图,已知AB∥CF,DE=EF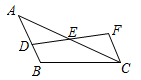 (1)、求证:△ADE≌△CFE;(2)、若AB=7,CF=4,求BD长.21. 如图:在△ABC中,已知∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M连接MD,过点D作DN⊥MD,交BM于点N.
(1)、求证:△ADE≌△CFE;(2)、若AB=7,CF=4,求BD长.21. 如图:在△ABC中,已知∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M连接MD,过点D作DN⊥MD,交BM于点N. (1)、求证:△DBN≌△DCM;(2)、设CD与BM相交于点E,若点E是CD的中点,试探究线段NE、ME、CM之间的数量关系,并证明你的结论.22. 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)、求证:△DBN≌△DCM;(2)、设CD与BM相交于点E,若点E是CD的中点,试探究线段NE、ME、CM之间的数量关系,并证明你的结论.22. 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
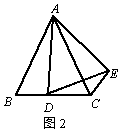

 (1)、如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)、设 , .
(1)、如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)、设 , .①如图2,当点在线段BC上移动,则 , 之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则 , 之间有怎样的数量关系?请直接写出你的结论.
23. 阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化到△ADF中即可判断. (1)、AB、AD、DC之间的等量关系为;(2)、完成(1)的证明.
(1)、AB、AD、DC之间的等量关系为;(2)、完成(1)的证明.问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
24. 如图 (1)、如图①,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;(2)、如图②,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)、如图③,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
(1)、如图①,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;(2)、如图②,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)、如图③,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.