浙江省台州市“海山教育联盟”2019-2020学年九年级上学期期中数学试题

试卷更新日期：2019-12-17 类型：期中考试

进入出卷网下载

一、单选题

1. 抛物线 $y ＝（ x ﹣ 2 ）^{2} + 3$ 的顶点坐标是（）

A、（2，3） B、（-2，3） C、（2，-3） D、（-2，-3）

查看试题解析
2. 已知⊙O的半径为3cm，OP＝4cm，则点P与⊙O的位置关系是（）

A、点P在圆内 B、点P在圆上 C、点P在圆外 D、无法确定

查看试题解析
3. 用配方法解一元二次方程x²﹣6x﹣8＝0，下列变形正确的是（）

A、（x﹣6）²＝﹣8+36 B、（x﹣6）²＝8+36 C、（x﹣3）²＝8+9 D、（x﹣3）²＝﹣8+9

查看试题解析
4. 如图，A，B是两座灯塔，在弓形AmB内有暗礁，游艇C在附近海面游弋，且∠AOB＝80°，要使游艇C不驶入暗礁区，则航行中应保持∠ACB（）

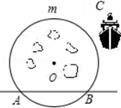A、小于40° B、大于40° C、小于80° D、大于80°

查看试题解析
5. 由于受非洲猪瘟的影响,今年4月份鸡的价格两次大幅下降.由原来每斤12元连续两次降价a%后售价下调到每斤7元,下列所列方程中正确的是（）

A、12(1+a%)2=7 B、12(1+a $^{2}$ %)=7 C、12(1+2a%) $^{2}$ =7 D、12(1−a%) $^{2}$ =7

查看试题解析
6. 如图，m∥n，点A在直线n上，以A为圆心的圆弧与直线n，m相交于B，C，若 $∠ CAB = 30 °$ ，则 $∠ ABC$ 的度数为（）

A、 $45 °$ B、 $60 °$ C、 $70 °$ D、 $75 °$

查看试题解析
7. 在抛物线y= $a x^{2}$ ﹣2ax﹣3a上有A（﹣0.5， $y_{1}$ ）、B（2， $y_{2}$ ）和C（3， $y_{3}$ ）三点，若抛物线与y轴的交点在正半轴上，则 $y_{1}$ 、 $y_{2}$ 和 $y_{3}$ 的大小关系为（）

A、 $y_{3}$ ＜ $y_{1}$ ＜ $y_{2}$ B、 $y_{3}$ ＜ $y_{2}$ ＜ $y_{1}$ C、 $y_{2}$ ＜ $y_{1}$ ＜ $y_{3}$ D、 $y_{1}$ ＜ $y_{2}$ ＜ $y_{3}$

查看试题解析
8. 如图，OA⊥OB，等腰直角三角形CDE的腰CD在OB上，∠ECD=45°，将三角形CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则 $\frac{OC}{CD}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
9. 将抛物线 $y = x^{2} - 6 x$ 绕原点旋转180度，则旋转后的抛物线解析式为（）

A、 $y = {(x - 3)}^{2} + 9$ B、 $y = {(x + 3)}^{2} + 9$ C、 $y = - {(x + 3)}^{2} + 9$ D、 $y = - {(x - 3)}^{2} + 9$

查看试题解析
10. 已知函数y＝2x与y＝x²﹣c(c为常数，﹣1≤x≤2)的图象有且仅有一个公共点，则常数c的值为（）

A、0＜c≤3或c＝﹣1 B、﹣l≤c＜0或c＝3 C、﹣1≤c≤3 D、﹣1＜c≤3且c≠0

查看试题解析

二、填空题

11. 已知 $x^{k - 2} - 4 x - 5 = 0$ 是一元二次方程，则k=.

查看试题解析
12. 如图，圆O的半径为2.C₁是函数y=x²的图象，C₂是函数y=−x²的图象，则阴影部分的面积是.

查看试题解析
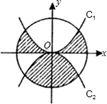13. 如图，已知O的半径为13，弦AB长为24，则点O到AB的距离是.

查看试题解析
14. 如图所示，在△ABC中，∠C＝90°，AC＝BC＝4cm.若以AC的中点O为旋转中心，将这个三角形旋转180°后，点B落在B′处，则BB′＝cm.

查看试题解析
15. 已知二次函数 $y = 2 x^{2} - 8 x + 11$ ，当自变量 $1 \leq x \leq 4$ 时，则y的取值范围为.

查看试题解析
16. 在矩形ABCD中，AB＝3，BC＝4，点E、F分别在BC与CD上，且∠EAF＝45°.如图甲，若EA＝EF，则EF＝；如图乙，若CE＝CF，则EF＝.

查看试题解析

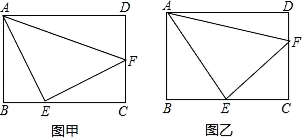
三、解答题

17. 解方程：

(1)、 $x^{2} - 4 x - 5 = 0$ ；

(2)、 $x^{2} - 2 x = 1$

查看试题解析
18. 如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0）、C（﹣1，0）．

(1)、①画出△ABC关于原点成中心对称的三角形△A′B′C′；
②将△ABC绕坐标原点O逆时针旋转90°，画出图形，直接写出点B的对应点B″的坐标；

(2)、请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．

查看试题解析
19. 已知关于x的方程 $m x^{2} - x - 1 = 0$ 有两个不相等的实数根，

(1)、求m的取值范围；

(2)、若方程的一个根是1，求方程的另一个根及m的值.

查看试题解析
20. 如图，已知二次函数 $y_{1} = a x^{2} + b x + c$ 的图像经过点 $A (- 1 ， 0)$ ， $C (0 ， 3)$ ，且对称轴为直线 $x = - 2$ ，一次函数 $y_{2} = m x + n$ 的图像经过 $A ， B$ 两点.

(1)、求二次函数的解析式；

(2)、若点 $B ， C$ 关于抛物线的对称轴对称，根据图像直接写出满足 $y_{1} \geq y_{2}$ 时 $x$ 的取值范围.

查看试题解析
21. 如图，AB为⊙O的直径，直线1切⊙O于点D，过点B作BH⊥1于点H，交⊙O于点C，连接BD．

(1)、求证：BD平分∠ABH；

(2)、若AB=10，BC=6.求点D到AB的距离.

查看试题解析
22. 如图①，AB是圆O的一条弦，点C是优弧 $\overset{⌢}{A m B}$ 上一点.

(1)、若∠ACB=45°，点P是O上一点(不与A． B重合)，则∠APB=；

(2)、如图②，若点P是弦AB与 $\overset{⌢}{A m B}$ 所围成的弓形区域(不含弦AB与 $\overset{⌢}{A m B}$ )内一点.求证：∠APB>∠ACB；

(3)、请在图③中直接用阴影部分表示出在弦AB与 $\overset{⌢}{A m B}$ 所围成的弓形区域内满足
$∠ A C B < ∠ A P B < 2 ∠ A C B$ 的点P所在的范围；

(4)、在（1）的条件下，以PB为边，向右作等腰直角三角形PBQ，连结AQ，如图4，已知AB=2，
①当点Q在线段AB的延长线上时，线段AQ的长为

②线段AQ的最小值为

查看试题解析

23. 周老师家的红心猕猴桃深受广大顾客的喜爱，猕猴桃成熟上市后，她记录了15天的销售数量和销售单价，其中销售单价y（元/千克）与时间第x天（x为整数）的数量关系如图所示，日销量P（千克）与时间第x天（x为整数）的部分对应值如下表所示：

时间第x天	1	3	5	7	10	11	12	15
日销量P（千克）	320	360	400	440	500	400	300	0

(1)、求y与x的函数关系式，并写出自变量x的取值范围；

(2)、从你学过的函数中，选择合适的函数类型刻画P随x的变化规律，请直接写出P与x的函数关系式及自变量x的取值范围；

(3)、在这15天中，哪一天销售额达到最大，最大销售额是多少元；

(4)、周老师非常热爱公益事业，若在前5天，周老师决定每销售1千克红心猕猴桃就捐献a元给“环保公益项目”，且希望每天的销售额不低于2800元以维持各种开支，求a的最大值.

查看试题解析

24.

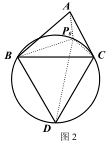
(1)、知识储备
①如图 1，已知点 P 为等边△ABC 外接圆的弧BC 上任意一点．求证：PB+PC= PA．

②定义：在△ABC 所在平面上存在一点 P，使它到三角形三顶点的距离之和最小，则称点 P 为△ABC的费马点，此时 PA+PB+PC 的值为△ABC 的费马距离．

(2)、知识迁移
①我们有如下探寻△ABC (其中∠A，∠B，∠C 均小于 120°)的费马点和费马距离的方法：

如图 2，在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆，根据(1)的结论，易知线段▲ 的长度即为△ABC 的费马距离.

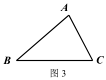
②在图 3 中，用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).

(3)、知识应用
①判断题（正确的打√，错误的打×）：

ⅰ.任意三角形的费马点有且只有一个（   ）；

ⅱ.任意三角形的费马点一定在三角形的内部（   ）.

②已知正方形 ABCD，P 是正方形内部一点，且 PA+PB+PC 的最小值为 $\sqrt{6} + \sqrt{2}$ ，求正方形 ABCD 的

边长．

查看试题解析