浙江省杭州市余杭区2019-2020学年九年级上学期期中数学试卷

试卷更新日期：2019-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 比较二次函数y＝2x²与y＝－ $\frac{1}{2}$ x²＋1，则（）

A、开口方向相同 B、开口大小相同 C、顶点坐标相同 D、对称轴相同

查看试题解析
2. 已知圆的半径为r ，圆外的点P到圆心的距离为d ，则（）

A、d＞r B、d＝r C、d＜r D、d≤r

查看试题解析
3. 如图，点A ， B ， C在 $⊙ O$ 上，若 $∠ B O C = 72^{\circ}$ ，则 $∠ B A C$ 的度数是（）

A、 $72^{\circ}$ B、 $36^{\circ}$ C、 $18^{\circ}$ D、 $54^{\circ}$

查看试题解析
4. 一个不透明的袋子里装有两双只有颜色不同的手套，小明已经摸出一只手套，他再任意摸取一只，恰好两只手套凑成同一双的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析
5. 一个扇形的弧长是10πcm，面积是60πcm² ，则此扇形的圆心角的度数是（）

A、300° B、150° C、120° D、75°

查看试题解析
6. 如图，三角形与⊙O叠合得到三条相等的弦AB、CD、EF，则以下结论正确的是（）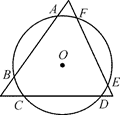

A、2∠AOB＝∠AEB B、 $\overset{⌢}{A B}$ ＝ $\overset{⌢}{C D}$ ＝ $\overset{⌢}{E F}$ C、 $\overset{⌢}{B C}$ ＝ $\overset{⌢}{D E}$ ＝ $\overset{⌢}{A F}$ D、点O是三角形三条中线的交点

查看试题解析
7. 已知关于x的二次函数y＝－(x－m)²＋2，当x＞1时，y随x的增大而减小，则实数m的取值范围是（）

A、m≤0 B、0＜m≤1 C、m≤1 D、m≥1

查看试题解析
8. 若点A(－ $\frac{13}{4}$ ，y₁)，B(－1，y₂)，C ( $\frac{5}{3}$ ，y₃)为二次函数y＝－x²－4x＋m的图象上的三个点，则y₁ ， y₂ ， y₃的大小关系为（）

A、y₂＞y₁＞y₃ B、y₁＞y₃＞y₂ C、y₃＞y₂＞y₁ D、y₂＞y₃＞y₁

查看试题解析
9. 如图，在△ABC中，∠C＝90°， $\overset{⌢}{D E}$ 的度数为α ，以点C为圆心，BC长为半径的圆交AB于点D ，交AC于点E ，则∠A的度数为（）

A、45º－ $\frac{1}{2}$ α B、 $\frac{1}{2}$ α C、45º＋ $\frac{1}{2}$ α D、25º＋ $\frac{1}{2}$ α

查看试题解析
10. 已知二次函数y＝x²－bx＋1(－1≤b≤1)，当b从－1逐渐变化到1的过程中，图象（）

A、先往左上方移动，再往左下方移动 B、先往左下方移动，再往左上方移动 C、先往右上方移动，再往右下方移动 D、向往右下方移动，再往右上方移动

查看试题解析

二、填空题

11. 甲、乙、丙三人排成一排，其中甲、乙两人位置恰好相邻的概率是.

查看试题解析

12. 二次函数y=ax²+bx+c（a≠0）的部分对应值如右表，则不等式ax²+bx+c＞0的解集为．

x	﹣3	﹣2	﹣1	0	1	2	3	4
y	6	0	﹣4	﹣6	﹣6	﹣4	0	6

查看试题解析

13. 如图，要拧开一个边长为a=6cm的正六边形螺帽，扳手张开的开口b至少为cm．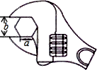

查看试题解析
14. 如图，A、B是⊙O上两点，弦AB＝a ， P是⊙O上不与点A、B重合的一个动点，连结AP、PB ，过点O分别作OE⊥AP于点E ， OF⊥PB于点F ，则EF＝． (用含a的代数式表示）．

查看试题解析
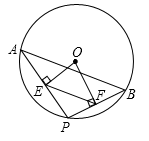15. 已知⊙O的半径OA＝r ，弦AB ， AC的长分别是 $\sqrt{2}$ r ， $\sqrt{3}$ r ，则∠BAC的度数为．

查看试题解析
16. 已知关于x的函数y=（m﹣1）x²+2x+m图象与坐标轴只有2个交点，则m=.

查看试题解析

三、解答题

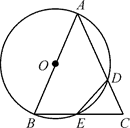
17. 已知二次函数的图象与x轴交于点(－1，0)和 (3，0)，并且与y轴交于点(0，3)．求这个二次函数表达式．

查看试题解析
18. 已知在△ABC中，AB＝AC ，以AB为直径的⊙O分别交AC于点 D ， BC于点E ，连接ED ．求证：ED＝EC ．

查看试题解析
19. 二次函数 y=ax²＋bx＋c(a≠0)的图象如图所示，根据图象解答下列问题：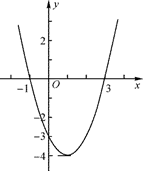

(1)、写出方程ax²＋bx＋c＝0(a≠0)的实数解；

(2)、若方程ax²＋bx＋c＝k有两个不相等的实数根，写出 k的取值范围；

(3)、当0＜x＜3 时，写出函数值y的取值范围.

查看试题解析
20. 一只不透明的袋子中，装有2个白球，1个红球，1个黄球，这些球除颜色外都相同．请用列表法或画树形图法求下列事件的概率：

(1)、搅匀后从中任意摸出1个球，恰好是白球．

(2)、搅匀后从中任意摸出2个球，2个都是白球．

(3)、再放入几个除颜色外都相同的黑球，搅匀后从中任意摸出1个球，恰好是黑球的概率为 $\frac{5}{7}$ ，求放入了几个黑球？

查看试题解析
21. 如图，在⊙O中，弦BC垂直于半径OA ，垂足为E ， D是优弧BC上一点，连结BD ， AD ， OC ， ∠ADB＝30°.

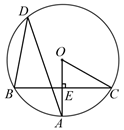(1)、求∠AOC的度数；

(2)、若弦BC＝6 cm，求图中劣弧BC的长．

查看试题解析
22. 如图，在同一平面直角坐标系中，二次函数y＝ax²＋bx＋c与二次函数y＝(a＋3)x²＋(b－15)x＋c＋18的图象与x轴的交点分别是A ， B ， C ．

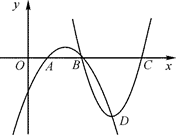(1)、判断图中经过点B ， D ， C的图象是哪一个二次函数的图象？试说明理由．

(2)、设两个函数的图象都经过点B、D ，求点B ， D的横坐标．

(3)、若点D是过点B、D、C的函数图象的顶点，纵坐标为－2，求这两个函数的解析式．

查看试题解析
23. 四边形ABCD是⊙O的内接四边形，连结AC、BD ，且DA＝DB ．

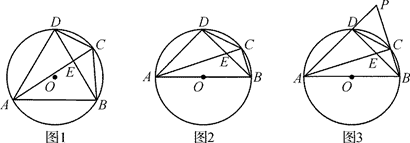(1)、如图1，∠ADB＝60°．求证：AC＝CD＋CB ．

(2)、如图2，∠ADB＝90°．
①求证：AC＝ $\sqrt{2}$ CD＋CB ．

②如图3，延长AD、BC交于点P ，且DC＝ $\sqrt{2}$ CB ，探究线段BD与DP的数量关系，并说明理由．

查看试题解析