浙江省杭州市萧山区城区片六校2019-2020学年九年级上学期期中数学试卷

试卷更新日期：2019-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 抛物线 $y = {(x - 2)}^{2} + 3$ 的对称轴是（）

A、直线x=-2 B、直线 x=2 C、直线x=-3 D、直线x=3

查看试题解析
2. 不透明袋子中有除颜色外完全相同的4个黑球和2个白球，从袋子中随机摸出3个球，下列事件是必然事件的是（）．

A、3个都是黑球 B、2个黑球1个白球 C、2个白球1个黑球 D、至少有1个黑球

查看试题解析
3. 如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=（）

A、8cm B、5cm C、3cm D、2cm

查看试题解析
4. 关于二次函数 $y = 2 x^{2} + 4 x - 1$ ，下列说法正确的是（）

A、图像与 $y$ 轴的交点坐标为 $(0 ， 1)$ B、图像的对称轴在 $y$ 轴的右侧 C、当 $x < 0$ 时， $y$ 的值随 $x$ 值的增大而减小 D、 $y$ 的最小值为-3

查看试题解析
5. 平移抛物线 $y = - 2 (x - 2) (x + 5)$ ，下列哪种平移方法不能使平移后的抛物线经过原点（）

A、向左平移2个单位 B、向右平移5个单位 C、向上平移10个单位 D、向下平移20个单位

查看试题解析
6. 已知一个正多边形的内角为a度，则下列不可能是a的值的是（）

A、90 B、100 C、120 D、176.4

查看试题解析
7. 已知点 $A (- 1, m), B (1, m), C (2, m - n) (n > 0)$ 在同一个函数的图象上，这个函数可能是（）

A、 $y ＝ x$ B、 $y = - \frac{2}{x}$ C、 $y ＝ x^{2}$ D、 $y ＝ ﹣ x^{2}$

查看试题解析
8. 如图，AB是⊙O的直径，OC是⊙O的半径，点D是半圆AB上一动点（不与A、B重合），连结DC交直径AB与点E，若∠AOC=60°，则∠AED的范围为（）

A、0°< ∠AED <180° B、30°< ∠AED <120° C、60°< ∠AED <120° D、60°< ∠AED <150°

查看试题解析
9. 如图，A、B、C、D、E是⊙O上的5等分点，连接AC、CE、EB、BD、DA ，得到一个五角星图形和五边形MNFGH ．有下列3个结论：① AO⊥BE， ② ∠CGD=∠COD+∠CAD， ③ BM=MN=NE．其中正确的结论是（）

A、① ② B、① ③ C、② ③ D、① ② ③

查看试题解析
10. 设函数 $y_{1} = (x - 2) (x - m)$ ， $y_{2} = \frac{3}{x}$ ，若当 $x = 1$ 时， $y_{1} = y_{2}$ ，则（）

A、当 $x > 1$ 时， $y_{1} < y_{2}$ B、当 $x < 1$ 时， $y_{1} > y_{2}$ C、当 $x < 0.5$ 时， $y_{1} < y_{2}$ D、当 $x > 5$ 时， $y_{1} > y_{2}$

查看试题解析

二、填空题

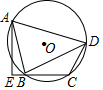
11. 抛物线 $y = x^{2} - 2 x - 1$ 与 $x$ 轴有个交点．

查看试题解析
12. 正方形ABCD是半径为10的圆内接正方形，则正方形的周长为．

查看试题解析
13. 同时掷两枚质地均匀的骰子，则至少有一枚骰子的点数是 $6$ 这个随机事件的概率为．

查看试题解析
14. 已知二次函数 $y = a {(x + b)}^{2} + c$ （ $a \neq 0$ ）图象的顶点在第二象限，且过点（1,0），则 $\frac{b + c}{a}$ 0（用“<、>、 $\geq$ 、 $\leq$ 、=”填写）．

查看试题解析
15. 如图，四边形ABCD内接于⊙O ， AE⊥CB交CB的延长线于点E ，若BA平分∠DBE ， AD＝5，CE＝ $\sqrt{13}$ ，则AE＝．

查看试题解析
16. 已知，AB、BC是半径为 $r$ 的⊙O内的两条弦，且AB=6，BC=8．（1）若∠ABC=90°，则 $r$ =；（2）若∠ABC=120°，则 $r$ =.

查看试题解析

三、解答题

17. 如图所示，△ABC的各顶点都在8×8的网格中的格点（即各个小正方形的顶点）上．

(1)、将线段BC绕图中F、G、H、M、N五个格点中的其中一个点可旋转到线段B₂C₂（点B的对应点为B₂）．则旋转中心是点．

(2)、将△ABC绕点A顺时针旋转90°得后到的△AB₁C₁ ．在图中画出△AB₁C₁ ．

查看试题解析
18. 在甲乙两个不透明的口袋中，分别有大小、材质完全相同的小球，其中甲口袋中的小球上分别标有数字1，2，3，4，乙口袋中的小球上分别标有数字2，3，4，先从甲袋中任意摸出一个小球，记下数字为m，再从乙袋中摸出一个小球，记下数字为n.

(1)、请用列表或画树状图的方法表示出所有（m，n）可能的结果；

(2)、若m，n都是方程x²﹣5x+6＝0的解时，则小明获胜；若m，n都不是方程x²﹣5x+6＝0的解时，则小利获胜，问他们两人谁获胜的概率大？

查看试题解析
19. 如图，⊙O的弦AB、CD的延长线相交于点P，且AB＝CD.求证PA＝PC.

查看试题解析
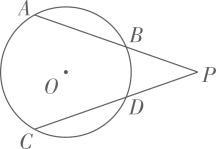20. 某农场拟建三间矩形牛饲养室，饲养室的一面全部靠现有墙(墙长为40m)，饲养室之间用一道用建筑材料做的墙隔开(如图)．已知计划中的建筑材料可建围墙的总长为60m，设三间饲养室合计长x(m)，总占地面积为y(m²)．

(1)、求y关于x的函数表达式和自变量的取值范围．

(2)、x为何值时，三间饲养室占地总面积最大？最大为多少？

查看试题解析
21. 已知：如图，OA是⊙O的半径，以OA为直径的⊙C与⊙O的弦AB相交于点D ，连结OD并延长交⊙O于点E ，连结AE ．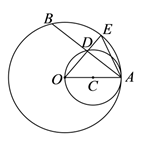

(1)、求证：AD=DB ．

(2)、若AO=10，DE=4，求AE的长．

查看试题解析
22. 已知抛物线 $y = x^{2} + a x + b$ 与 $x$ 轴的两个交点间的距离为2．

(1)、若此抛物线的对称轴为直线 $x = 1$ ，请判断点（3，3）是否在此抛物线上？

(2)、若此抛物线的顶点为（S，t），请证明 $t = - 1$ ；

(3)、当 $10 < a < 20$ 时，求 $b$ 的取值范围

查看试题解析
23. 如图，在△ABC中，AB=BC，∠ABC=90°，D是AB上一动点，连接CD，以CD为直径的⊙M交AC于点E，连接BM并延长交AC于点F，交⊙M于点G，连接BE．

(1)、求证：点B在⊙M上．

(2)、当点D移动到使CD⊥BE时，求BC：BD的值．

(3)、当点D到移动到使 $\overset{⌢}{C G} = 30^{0}$ 时，求证：AE²+CF²=EF²．

查看试题解析