浙江省杭州市拱墅区2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. 在Rt△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边，则（）

A、 $sin A = \frac{a}{b}$ B、 $cos A = \frac{a}{c}$ C、 $sin B = \frac{b}{c}$ D、 $tan B = \frac{a}{b}$

查看试题解析
2. 下列事件中,属于不可能事件的是（）

A、掷一枚骰子,朝上一面的点数为5 B、任意画一个三角形,它的内角和是178° C、任意写一个数,这个数大于-1 D、在纸上画两条直线,这两条直线互相平行

查看试题解析
3. 如图，点A、B、C在⊙O上，∠ACB=40°，则（）

A、∠AOB=80°，弧AB=80° B、∠AOB=80°，弧AB=40° C、∠AOB=40°，弧AB=80° D、∠AOB=40°，弧AB=40°

查看试题解析
4. 关于二次函数y=3x²-6，下列叙述正确的是（）

A、当 $x = 3$ 时，y有最大值 $- 6$ B、当 $x = 3$ 时，y有最小值 $- 6$ C、当 $x = 0$ 时，y有最大值 $- 6$ D、当 $x = 0$ 时，y有最小值 $- 6$

查看试题解析
5. 如图，直线l₁∥l₂∥l₃ ，直线AC交l₁、l₂、l₃于点A、B、C ，直线DF交l₁、l₂、l₃于点D、E、F ，已知 $\frac{B C}{A C} = \frac{3}{7}$ ，若DE=3，则DF的长是（）

A、 $\frac{9}{4}$ B、4 C、 $\frac{21}{4}$ D、7

查看试题解析
6. 已知圆心角为120°的扇形的弧长为6π，该扇形的面积为（）

A、 $18 π$ B、 $27 π$ C、 $36 π$ D、 $54 π$

查看试题解析
7. 如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，DE∥BC ， DF∥AC ，若△ADE与四边形DBCE的面积相等，则△DBF与△ADE的面积之比为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\sqrt{2} - 1$ D、3-2 $\sqrt{2}$

查看试题解析
8. 在平面直角坐标系中有两点A（﹣2，4）、B（2，4），若二次函数y＝ax²﹣2ax﹣3a（a≠0）的图象与线段AB只有一个交点，则（）

A、a的值可以是 $- \frac{4}{3}$ B、a的值可以是 $\frac{3}{5}$ C、a的值不可能是﹣1.2 D、a的值不可能是1

查看试题解析
9. 如图，AB是⊙O的直径，点C是圆上任意一点，点D是AC中点，OD交AC于点E ， BD交AC于点F ，若BF＝1.25DF ，则tan∠ABD的值为（）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{3}{5}$ D、 $\frac{\sqrt{5}}{4}$

查看试题解析

二、填空题

10. 任意抛掷—枚质地均匀的骰子,朝上面的点数能被3整除的概率是.

查看试题解析
11. 计算：cos²45°-tan30°sin60°= ．

查看试题解析
12. 铁路道口的栏杆如图所示，AO=16.5米，CO=1.25米，当栏杆C端下降的垂直距离（CD）为0.5米时，栏杆A端上升的垂直距离（AB）为米．

查看试题解析
13. 函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图像如图所示，则方程 $a x^{2} + b x + c = 3$ 的解是.

查看试题解析
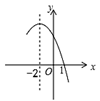14. 如图是一个圆拱形隧道的截面，若该隧道截面所在圆的半径为3.5米，路面宽AB为4.2米，则该隧道最高点距离地面米．

查看试题解析
15. 如图，已知Rt△ABC中，∠B=90°，∠A=60°，AC=2 $\sqrt{3}$ +4，点M、N分别在线段AC、AB上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为．

查看试题解析

三、解答题

16. 已知二次函数y=2x²+bx+1的图象过点（2，3）．

(1)、求该二次函数的表达式；

(2)、若点P（m ， m²+1）也在该二次函数的图象上，求点P的坐标．

查看试题解析
17. 如图，某轮船在海上向正东方向航行，上午8：00在点A处测得小岛O在北偏东60°方向，之后轮船继续向正东方向行驶1.5行驶到达B处，这时小岛O在船的北偏东30°方向。

(1)、求轮船从A处到B处的航速；

(2)、如果轮船按原速继续向东航行，还需经过多少时间轮船才恰好位于小岛的东南方向?

查看试题解析
18. 把9个只有颜色不同的小球分别装入甲乙丙三个布袋里其中甲布袋里有3个红球，1个白球；乙布袋里有1个红球，2个白球；丙布袋里有1个红球，1个白球．

(1)、从甲布袋中随机摸出1个小球，摸出的小球是红球的概率是多少？

(2)、用列表法或画树状图，解决下列问题：
①从甲、乙两个布袋中随机各摸出1个小球，求摸出的两个小球都是红球的概率；

②从甲、乙、丙三个布袋中随机各摸出1个小球，求摸出的三个小球是一红二白的概率．

查看试题解析
19. 如图，在△ABC中，AB=8，AC=6.点D在边AB上，AD=4.5.△ABC的角平分线AE交CD于点F.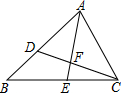

(1)、求证：△ACD∽△ABC；

(2)、求 $\frac{A F}{A E}$ 的值.

查看试题解析
20. 如图，四边形ABCD内接于⊙O ， BC=CD ， ∠C=2∠BAD ．

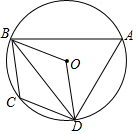(1)、求∠BOD的度数；

(2)、求证：四边形OBCD是菱形；

(3)、若⊙O的半径为r ， ∠ODA=45°，求△ABD的面积（用含r的代数式表示）．

查看试题解析
21. 如图，要在一面靠墙（墙长11米）的空地上，用长为16米的篱笆围成一个矩形花圃（靠墙一边不超过墙长），设与墙平行的一边BC的长为x米，面积为y平方米．

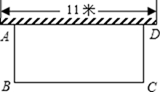(1)、直接写出：与墙垂直的一边AB的长；（用含x的代数式表示）

(2)、若矩形花圃的面积为30平方米，求BC的长；

(3)、若与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度，问BC边应为多少米时，才能使矩形花圃ABCD所占地面面积最小，并求出此时最小的面积．

查看试题解析
22. 如图，在△ABC中，AB=AC ，以AB为直径的⊙O分别交BC ， AC于点D ， E ，连结EB ，交OD于点F ．

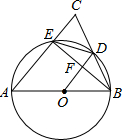(1)、求证：OD⊥BE ．

(2)、若DE= $\sqrt{6}$ ，AB=6，求AE的长．

(3)、若△CDE的面积是△OBF面积的 $\frac{2}{3}$ ，求线段BC与AC长度之间的等量关系，并说明理由．

查看试题解析