浙江省杭州市江干区2018-2019学年九年级上学期期末数学试卷
试卷更新日期：2019-12-16 类型：期末考试
一、单选题
-
1. 下列函数是二次函数的是（ ）.A、y＝2x B、y= +x C、y＝x+5 D、y＝(x+1)(x﹣3)2. 由5a＝6b(a≠0)，可得比例式（ ）.A、 = B、 = C、 D、3. 二次函数y＝﹣2(x﹣1)2+3的最大值是（ ）.A、﹣2 B、1 C、3 D、﹣14. 学校组织校外实践活动，安排给九年级两辆车，小明与小慧都可以从两辆车中任选一辆搭乘，则小明和小慧乘同一辆车的概率是（ ）.A、 B、 C、 D、15. 如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝110°，则∠α＝（ ）
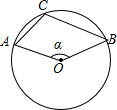A、70° B、110° C、120° D、140°6. 如图，E是平行四边形ABCD的BA边的延长线上的一点，CE交AD于点F．下列各式中，错误的是（ ）.
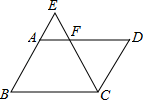A、 B、 C、 D、7. 若抛物线y＝ax2+2ax+4a(a＞0)上有A( ，y1)、B(2，y2)、C( ，y3)三点，则y1、y2、y3的大小关系为（ ）.A、y1＜y2＜y3 B、y1＜y3＜y2 C、y3＜y1＜y2 D、y2＜y3＜y18. 四位同学在研究函数y＝ax2+bx+c(a、b、c为常数，且a≠0)时，甲发现当x＝1时，函数有最大值；乙发现﹣1是方程ax2+bx+c＝0的一个根；丙发现函数的最大值为﹣1；丁发现当x＝2时，y＝﹣2，已知四位中只有一位发现的结论时错误的，则该同学是（ ）.A、甲 B、乙 C、丙 D、丁9. 已知，如图一张三角形纸片ABC，边AB长为10cm，AB边上的高为15cm，在三角形内从左到右叠放边长为2的正方形小纸片，第一次小纸片的一条边都在AB上，依次这样往上叠放上去，则最多能叠放的正方形的个数是（ ）.
A、12 B、13 C、14 D、1510. 如图，把边长为4的正方形ABCD绕A点顺时针旋转30°得到正方形AB′C′D′，边B′C′与DC交于点O，则四边形AB′OD的周长是（ ）.
A、12 B、8+ C、8+ D、8+二、填空题
-
11. 已知b是a、c的比例中项，若a＝4，c＝9，那么b＝ ．12. 如图，已知正三角形ABC，分别以A、B、C为圆心，以AB长为半径画弧，得到的图形我们称之为弧三角形．若正三角形ABC的边长为1，则弧三角形的周长为 ．
13. 如图，AB是⊙O的直径，E是OB的中点，过E点作弦CD⊥AB，G是弧AC上任意一点，连结AG、GD，则∠G＝ ．
14. 如图所示矩形ABCD中，AB＝4，BC＝3，P是线段BC上一点(P不与B重合)，M是DB上一点，且BP＝DM，设BP＝x，△MBP的面积为y，则y与x之间的函数关系式为 ．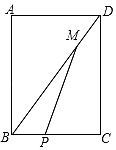
15. 如图，有一矩形纸片ABCD，AB＝6，AD＝8，将纸片折叠，使AB落在AD边上，折痕为AE，再将△AEB以BE为折痕向右折叠，AE与DC交于点F，则 的值是 ．
16. 如图，正六边形ABCDEF中，P是边ED的中点，连接AP，则 ＝ ．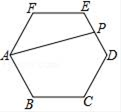
三、解答题
-
17. 如图，一个人拿着一把长为12cm的刻度尺站在离电线杆20m的地方．他把手臂向前伸直，尺子竖直，尺子两端恰好遮住电线杆，已知臂长约为40m，求电线杆的高度．
18. 某水果公司以2元千克的成本购进1000千克柑橘，销售人员从柑橘中抽取若干柑橘统计损坏情况，结果如下表：柑橘总质量
损坏柑橘质量
柑橘损坏的频率
50
5.5
0.110
100
10.5
0.105
150
15.15
0.101
200
19.42
0.097
250
24.25
0.097
300
30.93
0.130
350
35.32
0.101
400
39.24
0.098
450
44.57
0.099
500
51.42
0.103
(1)、请根据表格中的数据，估计这批柑橘损坏的概率(精确到0.01)；(2)、公司希望这批柑橘能够至少获利500元，则毎千克最低定价为多少元？(精确到0.1元)．19. 花圃用花盆培育某种花苗，经过试验发现，毎盆的盈利与毎盆的株数构成一种函数关系．每盆植入2株，每株盈利4元，以同样的栽培条件，当株数在2到9株之间时，若每盆增加一株，平均单株盈利就减少0.5元．要使每盆盈利达到最大，应该植多少株？20. 如图，在△ABC中，AB＝AC，以腰AB为直径作半圆，分别交BC、AC于点D、E，连结DE．
(1)、求证：BD＝DE；(2)、若AB＝13，BC＝10，求CE的长．
