浙江省杭州市西湖区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-12-16 类型:期末考试
一、单选题
-
1. 已知 = ,则 的值为( )A、 B、 C、 D、2. 如图,点A,B,P是⊙O上的三点,若 ,则∠APB的度数为( )
 A、80° B、140° C、20° D、50°3. 下列每个选项中的两个图形一定相似的是( )A、任意两个矩形 B、两个边长不等的正五边形 C、任意两个平行四边形 D、两个等腰三角形4.
A、80° B、140° C、20° D、50°3. 下列每个选项中的两个图形一定相似的是( )A、任意两个矩形 B、两个边长不等的正五边形 C、任意两个平行四边形 D、两个等腰三角形4.在一个不透明的盒子中装有8个白球,若干个黄球,它们除颜色不同外,其余均相同,若从中随机摸出一个球为白球的概率是 ,则黄球的个数为( ).
A、16 B、12 C、8 D、45. 将二次函数y=5x2的图象先向右平移2个单位,再向下平移3个单位,得到的函数图象的解析式为( )A、y=5(x+2)2+3 B、y=5(x﹣2)2+3 C、y=5(x+2)2﹣3 D、y=5(x﹣2)2﹣36. 如图,正方形OABC的边长为8,点P在AB上,CP交OB于点Q . 若S△BPQ= ,则OQ长为( )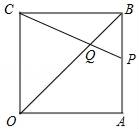 A、6 B、6 C、 D、7. 一元二次方程x2+bx+c=0有一个根为x=3,则二次函数y=2x2﹣bx﹣c的图象必过点( )A、(﹣3,0) B、(3,0) C、(﹣3,27) D、(3,27)8. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于( )
A、6 B、6 C、 D、7. 一元二次方程x2+bx+c=0有一个根为x=3,则二次函数y=2x2﹣bx﹣c的图象必过点( )A、(﹣3,0) B、(3,0) C、(﹣3,27) D、(3,27)8. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于( ) A、 B、 C、4 D、39. 对于代数式ax2+bx+c(a≠0),下列说法正确的是( )
A、 B、 C、4 D、39. 对于代数式ax2+bx+c(a≠0),下列说法正确的是( )①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则a +bx+c=a(x-p)(x-q)②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
A、③ B、①③ C、②④ D、①③④10. 在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片ABCD可以进行如下操作:①把△ABF翻折,点B落在C边上的点E处,折痕为AF , 点F在BC边上;②把△ADH翻折,点D落在AE边上的点G处,折痕为AH , 点H在CD边上,若AD=6,CD=10,则 =( )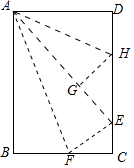 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
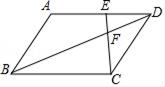
11. 抛物线y=2x2﹣2x与x轴的交点坐标为 .12. 一个密码箱的密码,每个数位上的数都是从0到9的自然数,若要使一次拨对的概率小于 ,则密码的位数至少要设置位.13. 把10cm长的线段进行黄金分割后得两条线段,其中较长的线段的长为cm .14. 如图,平行四边形ABCD中,点E是AD边上一点,连结EC、BD交于点F , 若AE:ED=5:4记△DFE的面积为S1 , △BCF的面积为S2 , △DCF的面积为S3 , 则DF:BF= , S1:S2:S3= .
 15. 已知抛物线y=﹣x2﹣3x+3,点P(m , n)在抛物线上,则m+n的最大值是 .
15. 已知抛物线y=﹣x2﹣3x+3,点P(m , n)在抛物线上,则m+n的最大值是 .三、解答题
-
16. 求半径为3的圆的内接正方形的边长.17. 在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x , 再从乙袋中随机抽取一个小球,记录标有的数字为y , 确定点M坐标为(x , y).(1)、用树状图或列表法列举点M所有可能的坐标;(2)、求点M(x , y)在函数y=﹣x+1的图象上的概率.18. 如图,在△ABC中,AD⊥BC , AD2=BD•CD , 记△ADB的面积为S△ADB , △CDA的面积为S△CDA .
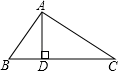 (1)、求证:△ADB∽△CDA;(2)、若S△ADB:S△CDA=1:4,求tanB .19. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
(1)、求证:△ADB∽△CDA;(2)、若S△ADB:S△CDA=1:4,求tanB .19. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
(1)、当x=4时,求y的值;(2)、当y<10时,求x的取值范围.20. 如图,已知△ABC中,AB=BC , AC=2,cosA= .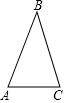 (1)、求BC与BC边上高的长;(2)、设边BC的垂直平分线与边AB的交点为D , 求 的值.21. 已知两个函数:y1=ax+4,y2=a(x﹣ )(x﹣4)(a≠0).(1)、求证:y1的图象经过点M(0,4);(2)、当a>0,﹣2≤x≤2时,若y=y2﹣y1的最大值为4,求a的值;(3)、当a>0,x<2时,比较函数值y1与y2的大小.22. 如图所示,在△ABC中,AB=AC=5,O为BC边中点,BC=8,点E、G是线段AB上的动点(不与端点重合),点H、F是线段AC上的动点,且EF∥GH∥BC . 设点O到EF、GH的距离分别为x、y .
(1)、求BC与BC边上高的长;(2)、设边BC的垂直平分线与边AB的交点为D , 求 的值.21. 已知两个函数:y1=ax+4,y2=a(x﹣ )(x﹣4)(a≠0).(1)、求证:y1的图象经过点M(0,4);(2)、当a>0,﹣2≤x≤2时,若y=y2﹣y1的最大值为4,求a的值;(3)、当a>0,x<2时,比较函数值y1与y2的大小.22. 如图所示,在△ABC中,AB=AC=5,O为BC边中点,BC=8,点E、G是线段AB上的动点(不与端点重合),点H、F是线段AC上的动点,且EF∥GH∥BC . 设点O到EF、GH的距离分别为x、y .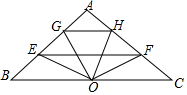 (1)、若△EOF的面积为S:
(1)、若△EOF的面积为S:①用关于x的代数式表示线段EF的长;
②求S的最大值;
(2)、以点O为圆心,当以OE为半径的圆与以OG为半径的圆重合时,求x与y应满足的关系式,并求x的取值范围.