浙江省杭州市下城区2018-2019学年九年级上学期期末数学试卷

试卷更新日期：2019-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. 在Rt△ABC中，∠C＝90°，AB＝5，AC＝3，则sinB的值是（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{5}{3}$

查看试题解析
2. 下列命题中是真命题的为（）

A、弦是直径 B、直径相等的两个圆是等圆 C、平面内的任意一点不在圆上就在圆内 D、一个圆有且只有一条直径

查看试题解析
3. 已知二次函数y＝ax²+4x+c ，当x等于﹣2时，函数值是﹣1；当x＝1时，函数值是5．则此二次函数的表达式为（）

A、y＝2x²+4x﹣1 B、y＝x²+4x﹣2 C、y＝﹣2x²+4x+1 D、y＝2x²+4x+1

查看试题解析
4. 下列是任意抛掷一枚质地均匀的正六面体骰子所得结果，其中发生的可能性很大的是（）

A、朝上的点数为2 B、朝上的点数为7 C、朝上的点数不小于2 D、朝上的点数为3的倍数

查看试题解析
5. 若a：b＝c：d ，则下列各式成立的是（）

A、a：d＝c：b B、b：d＝c：a C、 $\frac{a + b}{b} = \frac{c - d}{d}$ D、 $\frac{a}{b} = \frac{a + c}{b + d}$ （ b+d≠0）

查看试题解析
6. 如图，在△ABC中，∠ACB＝90°，分别以AC ， BC ， AB为直径作半圆，记三个半圆的弧长分别为m ， n ， l ，则下列各式成立的是（）

A、m+n＜l B、m+n＝l C、m²+n²＞l² D、m²+n²＝l²

查看试题解析
7. 在△ABC中，D ， E分别为BC ， AC上的点，且AC＝2EC ，连结AD ， BE ，交于点F ．设x＝CD：BD ， y＝AF：FD ，则（）

A、y＝x+1 B、y＝ $\frac{4}{3}$ x+1 C、y＝ $\frac{x + 1}{x}$ D、y＝ $\frac{2 - x}{1 - x}$

查看试题解析
8. 在一个不透明的布袋中装有4个只有标号不一样的球，从中任取两个球，设所得球上两个标号的数字的积为k ，并记事件“2，8，k三个数中正好有一个数为另两个数的比例中项”为 A ．若4个球上所标的数字分别为 $\frac{1}{2}$ ，1，3，4，则P（A）＝（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{3}{8}$

查看试题解析
9. 已知二次函数y＝（a﹣1）x²+3ax+1图象上的四个点的坐标为（x₁ ， m），（x₂ ， m），（x₃ ， n），（x₄ ， n），其中m＜n ．下列结论可能正确的是（）

A、若a＞ $\frac{3}{2}$ ，则 x₁＜x₂＜x₃＜x₄ B、若a＞ $\frac{3}{2}$ ，则 x₄＜x₁＜x₂＜x₃ C、若a＜﹣ $\frac{3}{2}$ ，则 x₁＜x₃＜x₂＜x₄ D、若a＜﹣ $\frac{3}{2}$ ，则 x₃＜x₂＜x₁＜x₄

查看试题解析
10. 已知△ABC内接于⊙O ，连接OA ， OB ， OC ，设∠OAC＝α，∠OBA＝β，∠OCB＝γ．则下列叙述中正确的有（）
①若α＜β，α＜γ，且OC∥AB ，则γ＝90°﹣α；②若α：β：γ＝1：4：3，则∠ACB＝30°；③若β＜α，β＜γ，则α+γ﹣β＝90°；④若β＜α，β＜γ，则∠BAC+∠ABC＝α+γ﹣2β．

A、①② B、③④ C、①②③ D、①②③④

查看试题解析

二、填空题

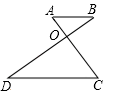
11. 如图，已知AB∥CD ， AC ， BD交于点O ，若AB：CD＝1：2，AO＝3，则OC＝．

查看试题解析
12. “手机阅读”已逐渐成了眼科病的主要病因，据调查表明在“中年人”中有“手机阅读”习惯的占比约达66%.若随机选择150名“中年人”进行调查，则估计有人有此习惯.

查看试题解析
13. 在△ABC中，（cosA﹣ $\frac{1}{2}$ ）²+|tanB﹣1|＝0，则∠C＝．

查看试题解析
14. 若圆内接正六边形的两条对角线长为m ， n（m＜n），则m：n＝．

查看试题解析
15. 已知函数y₁＝﹣（m+1）x²+nx+2与y₂＝mx+2的图象都经过A（4，﹣4）．若y₂≤y₁ ，则x的取值范围为．

查看试题解析
16. 已知P为⊙O外的一点，P到⊙O上的点的最大距离为6，最小距离为2．若AB为⊙O内一条长为1的弦，则点P到AB的距离的最大值为，最小值为．

查看试题解析

三、解答题

17. 为了有效保护环境，某景区要求游客将垃圾按可回收垃圾，不可回收垃圾，有害垃圾分类投放．一天，小林一家游玩了该景区后，把垃圾按要求分成三袋并随机投入三类垃圾桶中，请用列树状图的方法求三袋垃圾都投对的概率．

查看试题解析
18. 如图，四边形ABGH ，四边形BCFG ，四边形CDEF都是正方形．请在图中找出与△HBC相似的三角形，并说明它们相似的理由．

查看试题解析
19. 如图，汽车在一条南北走向的公路上以每小时60千米的速度匀速向北行驶．当汽车在A处时，某信号塔C在它的北偏西30°方向，汽车前行2分钟．到达B处，此时信号塔C在它的北偏西45°方向．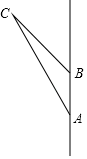

(1)、求AB的距离．

(2)、求信号塔C到该公路的距离．（ $\sqrt{3} \approx 1.73$ ，结果精确到0.1千米）

查看试题解析
20. 一个斜抛物体的水平运动距离为x（m），对应的高度记为h（m），且满足h＝ax²+bx﹣11a（其中a≠0）．已知当x＝0时，h＝2；当x＝10时，h＝2．

(1)、求h关于x的函数表达式．

(2)、求斜抛物体的最大高度和达到最大高度时的水平距离．

查看试题解析
21. 在⊙O中， $\overset{⌢}{A B}$ 的度数为120°，点P为弦AB上的一点，连结OP并延长交⊙O于点C ，连结OB ， AC ．

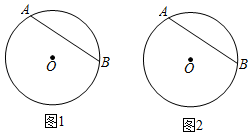(1)、若P为AB中点，且PC＝1，求圆的半径．

(2)、若BP：BA＝1：3，请求出tan∠OPA ．

查看试题解析
22. 已知二次函数y＝ax²+bx﹣3（a≠0），且a+b＝3．

(1)、若其图象经过点（﹣3，0），求此二次函数的表达式．

(2)、若（m ， n）为（1）中二次函数图象在第三象限内的点，请分别求m ， n的取值范围．

(3)、点P（x₁ ， y₁），Q（x₂ ， y₂）是函数图象上两个点，满足x₁+x₂＝2且x₁＜x₂ ，试比较y₁和y₂的大小关系．

查看试题解析
23. 如图，在△ABC中，∠C＝90°，D为AC上的一点，过D作DE⊥AC ，过B作BE⊥AB ， DE ， BE交于点 E ．已知BC＝3，AB＝5．

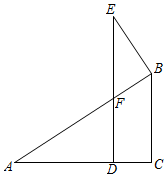(1)、证明：△EFB∽△ABC ．

(2)、若CD＝1，请求出ED的长．

(3)、连结AE ，记CD＝a ， △AFE与△EBF面积的差为b ．若存在实数t₁ ， t₂ ， m（其中t₁≠t₂），当a＝t₁或a＝t₂时，b的值都为m ．求实数m的取值范围．

查看试题解析