浙江省宁波市镇海区2019届九年级上学期期末质量检测数学试题

试卷更新日期：2019-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. 由等积式 $m a = n b$ 能得到比例式（）

A、 $\frac{a}{b} = \frac{m}{n}$ B、 $\frac{a}{b} = \frac{n}{m}$ C、 $\frac{m}{a} = \frac{n}{b}$ D、 $\frac{m}{b} = \frac{a}{n}$

查看试题解析
2. 下列事件中，属于不确定事件的是（）

A、抛掷一枚硬币，正面朝上 B、在空中抛掷石块，石块终将落下 C、小明的跑步速度是100米/秒 D、在一个标准大气压下，水到 $100^{\circ} C$ 就沸腾

查看试题解析
3. 如图，已知点 $A$ 、 $B$ 、 $C$ 都在 $⊙ O$ 上， $∠ C = 35^{\circ}$ ，则 $∠ A O B$ 的度数是（）

A、 $75^{\circ}$ B、 $70^{\circ}$ C、 $60^{\circ}$ D、 $35^{\circ}$

查看试题解析
4. 如图是一个正方体的表面展开图，则原正方体中与“建”字所在面的相对面上标的字是（）

A、美 B、丽 C、镇 D、海

查看试题解析
5. 在Rt△ABC中，∠C=90°，若sin∠A= $\frac{5}{13}$ ，则cos∠A的值为（　　）

A、 $\frac{12}{13}$ B、 $\frac{8}{13}$ C、 $\frac{2}{3}$ D、 $\frac{5}{12}$

查看试题解析
6. 如图，在△ABC中，点D、E分别在AB、AC上，DE∥BC，若AD＝2，DB＝1，△ADE、△ABC的面积分别为S₁、S₂ ，则 $\frac{S_{1}}{S_{2}}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{4}{9}$ D、2

查看试题解析
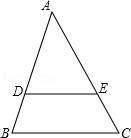7. 小明和小华参加社会实践活动，随机选择“打扫社区卫生”和“参加社会调查”其中一项，那么两人同时选择“参加社会调查”的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
8. 如图，已知圆O的半径为10，AB⊥CD，垂足为P，且AB＝CD＝16，则OP的长为（）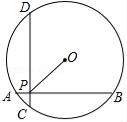

A、6 B、6 $\sqrt{2}$ C、8 D、8 $\sqrt{2}$

查看试题解析
9. 如图，已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点)，要使ΔABC∽ΔPBD，则点P的位置应落在

A、点 $P_{1}$ 上 B、点 $P_{2}$ 上 C、点 $P_{3}$ 上 D、点 $P_{4}$ 上

查看试题解析
10. 如图所示，在 $Δ A B C$ 中， $∠ A B C = 50^{\circ}$ ， $∠ A C B = 60^{\circ}$ ， $I$ 是 $Δ A B C$ 的内心，延长 $A I$ 交 $Δ A B C$ 的外接圆于点 $D$ ，则 $∠ I C D$ 的度数是（）

A、 $50^{\circ}$ B、 $55^{\circ}$ C、 $60^{\circ}$ D、 $65^{\circ}$

查看试题解析
11. 如图，△ABC中，AB=AC=5，BC=6，AD⊥BC于点D，点E是线段AD上一点，以点E为圆心，r为半径作⊙E．若⊙E与边AB，AC相切，而与边BC相交，则半径r的取值范围是（）

A、r＞ $\frac{5}{2}$ B、 $\frac{5}{2}$ ＜r≤4 C、 $\frac{3}{2}$ ＜r≤4 D、 $\frac{3}{2}$ ＜r≤ $\frac{12}{5}$

查看试题解析

二、填空题

12. 已知 $⊙ O$ 的半径为 $5 c m$ ，圆心 $O$ 到直线 $l$ 的距离为 $6 c m$ ，则直线 $l$ 与 $⊙ O$ 的位置关系是．

查看试题解析
13. 已知 $A$ 、 $B$ 两地在地图上的距离为 $10 c m$ ，地图上的比例尺为 $1 : 2000$ ，则 $A$ 、 $B$ 两地的实际距离是 $m$ ．

查看试题解析
14.
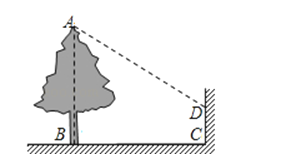
如图，当太阳光与地面上的树影成45°角时，树影投射在墙上的影高CD等于2米，若树根到墙的距离BC等于8米，则树高AB等于米．

查看试题解析
15. 如图，分别以等边三角形的每个顶点为圆心、以边长为半径，在另两个顶点间作一段圆弧，三段圆弧围成的曲边三角形称为勒洛三角形．若等边三角形的边长为a，则勒洛三角形的周长为．

查看试题解析
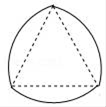16. 如图，已知在 $R t Δ A B C$ 中， $∠ C$ 为直角， $A C = 5$ ， $B C = 12$ ，在 $R t Δ A B C$ 内从左往右叠放边长为1的正方形小纸片，第一层小纸片的一条边都在 $A B$ 上，依次这样往上叠放上去，则第二层最多能叠放个正方形小纸片.

查看试题解析
17. 如图，正方形 $A B C D$ 和正 $Δ A E F$ 都内接于半径为1的 $⊙ O$ ， $E F$ 与 $B C$ 、 $C D$ 分别相交于点 $G$ 、 $H$ ，则 $G H$ 的长为.

查看试题解析

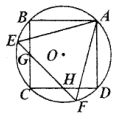
三、解答题

18. 计算： $\cos 45^{\circ} \cdot \tan 45^{\circ} + \sqrt{3} \cdot \tan 30^{\circ} - 2 \cos^{2} 30^{\circ}$

查看试题解析
19. 一个不透明的盒子里有 $n$ 个红球和6个黄球（每个球除颜色外其他完全相同）.

(1)、若从盒子里拿走 $m$ 个黄球，这时从盒子里随机摸出一个球是黄球的事件为“随机事件”，则 $m$ 的最大值为；

(2)、若在盒子中拿走4个黄球后进行摸球实验，每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大题重复摸球实验后发现，摸到黄球的频率稳定在 $50 %$ ，问 $n$ 的值是多少？

(3)、在（2）的条件下，若从盒子里同时摸出两个球，用树状图或列表法列举出所有可能，并求摸出的两个球都是黄球的概率.

查看试题解析
20. 有一个顶部是圆锥，底部是圆柱的粮囤模型，如图是它的主视图.

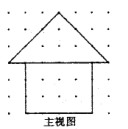(1)、画出该粮囤模型的俯视图；

(2)、若每相邻两个格点之间的距离均表示1米，请计算：
①在粮囤顶部铺上油毡，需要多少平方米油毡（油毡接缝重合部分不计）？

②若粮食最多只能装至与圆柱同样高，则最多可以存放多少立方米粮食？（结果保留 $π$ 和根号）

查看试题解析
21. 已知：如图，在 $Δ A B C$ 中， $∠ B A C = 90^{\circ}$ ， $A B = A C$ ，点 $D ， E$ 分别在 $B C$ ， $A C$ 上，且 $∠ A D E = 45^{\circ}$ .

(1)、求证： $Δ A B D ∽ Δ D C E$ ；

(2)、若 $A B = 2$ ， $B D = 1$ ，求 $C E$ 的长.

查看试题解析
22. 如图， $A B$ 为 $⊙ O$ 的直径， $C D ⊥ A B$ 于点 $E$ ，交 $⊙ O$ 于点 $D$ ， $O F ⊥ A C$ 于点 $F$ .

(1)、求证： $O F = \frac{1}{2} B D$ ；

(2)、当 $∠ D = 30^{\circ}$ ， $B C = 1$ 时，求圆中阴影部分的面积.

查看试题解析
23. 如图所示，某天我国一艘海监执法船在南海海域正在进行常态化巡航，在 $A$ 处发现在北偏东 $23^{\circ}$ 方向距离为20海里的 $B$ 处有一艘不明身份的船只正在向正东方向航行，便迅速沿北偏东 $60^{\circ}$ 的方向前往监视巡查，经过一段时间后，在 $C$ 处成功拦截不明船只.

(1)、求 $∠ B A C$ 及 $∠ C$ 的大小；

(2)、问不明船只从被发现到被拦截行驶了多少海里？此时海监执法船行驶了多少海里？（最后结果保留根号）（参考数据： $\cos 37^{\circ} = 0.8$ ， $\sin 37^{\circ} = 0.6$ ， $\tan 37^{\circ} = 0.75$ ）

查看试题解析
24. 如图，抛物线 $y = - \frac{3}{4} x^{2} + \frac{9}{4} x + 3$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ .在线段 $O A$ 上有一动点 $E (m ， 0)$ （不与 $O ， A$ 重合），过点 $E$ 作 $x$ 轴的垂线交 $A B$ 于点 $N$ ，交抛物线于点 $P$ ，过点 $P$ 作 $P M ⊥ A B$ 于点 $M$ .

(1)、求直线 $A B$ 的函数解析式；

(2)、求证： $Δ P M N ∽ Δ A E N$ ；并求出当 $m$ 为何值时， $Δ P M N$ 和 $Δ A E N$ 的相似比为 $\frac{6}{5}$ .

查看试题解析
25. 如图

(1)、如图1， $Δ A B C$ 的内切圆与边 $A B$ ， $A C$ ， $B C$ 分别相切于点 $D ， E ， F$ ，若 $∠ A C B = 90 °$ ， $A D = 3$ ， $B D = 4$ ，求 $Δ A B C$ 的面积 $S$ ；

(2)、观察（1）中所得结论中 $S$ 与 $A D$ ， $B D$ 之间的数量关系，猜测：若（1）中 $A D = m$ ， $B D = n$ ，其余条件不变，则 $Δ A B C$ 的面积为多少？并证明你的结论；

(3)、如图2，锐角 $Δ A B C$ 的内切圆与边 $A B ， A C ， B C$ 分别相切于点 $D ， E ， F$ ，若 $∠ A C B = 60^{\circ}$ ， $A D = m$ ， $B D = n$ ，求 $Δ A B C$ 的面积.（结果用含 $m ， n$ 的式子表示）

查看试题解析