浙江省绍兴市柯桥区2019届九年级上学期期末数学试题

试卷更新日期：2019-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列扑克牌中，中心对称图形有 $($ $)$

A、1张 B、2张 C、3张 D、4张

查看试题解析
2. 下列事件中，属于必然事件的是 $($ $)$

A、购买一张体育彩票，中奖 B、太阳从东边升起 C、2019年元旦是晴天 D、经过有交通信号灯的路口，遇到红灯

查看试题解析
3. 如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠C的度数为（）

A、116° B、58° C、42° D、32°

查看试题解析
4. 如果把一条线段分为两部分，使其中较长的一段与整个线段的比是黄金分割数，那么较短一段与较长一段的比也是黄金分割数．由此，如果设整个线段长为1，较长段为x，可以列出的方程为（）

A、 $\frac{1 - x}{x}$ = $\frac{x}{1}$ B、 $\frac{1 - x}{1}$ = $\frac{1}{x}$ C、 $\frac{x}{1 - x}$ = $\frac{1 - x}{1}$ D、 $\frac{1 - x}{x}$ = $\frac{x}{\sqrt{5}}$

查看试题解析
5. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米，木工要以一根长为60厘米的木条为一边，做一个与模型三角形相似的三角形，那么另两条边的木条长度不符合条件的是（）

A、30厘米、45厘米； B、40厘米、80厘米； C、80厘米、120厘米； D、90厘米、120厘米

查看试题解析
6. 如图， $∠ ABC = 70^{\circ}$ ，O为射线BC上一点，以点O为圆心， $\frac{1}{2} OB$ 长为半径做 $⊙ O$ ，要使射线BA与 $⊙ O$ 相切，应将射线绕点B按顺时针方向旋转（）

A、 $35^{\circ}$ 或 $70^{\circ}$ B、 $40^{\circ}$ 或 $100^{\circ}$ C、 $40^{\circ}$ 或 $90^{\circ}$ D、 $50^{\circ}$ 或 $110^{\circ}$

查看试题解析
7. 已知线段a，b，c，求作线段x，使 $x = \frac{ac}{b}$ ，下列作法中正确的是 $($ $)$

A、 B、 C、 D、

查看试题解析
8. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=m．若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积S的最大值为（）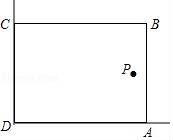

A、193 B、194 C、195 D、196

查看试题解析
9. 今有一副三角板如图，中间各有一个直径为2cm的圆洞，现用三角板a的 $30^{\circ}$ 角那一头插入三角板b的圆洞中，则三角板a通过三角板b的圆洞那一部分的最大面积为 $($ $) {cm}^{2} ($ 不计三角板厚度 $)$

A、 $2 + \sqrt{3}$ B、 $2 \sqrt{3}$ C、4 D、 $4 + \sqrt{3}$

查看试题解析

二、填空题

10. 如图，在 $Rt △ ABC$ 中， $∠ C = 90^{\circ}$ ， $AC = 4$ ， $BC = 8$ ，则 $tanB$ 的值是．

查看试题解析
11. 在一个不透明的袋中装有12个红球和若干个白球，它们除颜色外都相同 $.$ 从袋中随机摸出一个球，记下颜色后放回，并搅均，不断重复上述的试验共5000次，其中2000次摸到红球，请估计袋中大约有白球个 $.$

查看试题解析
12. 如图，AB、BC是 $⊙ O$ 的弦， $∠ A B C = 90^{\circ}$ ，OD、OE分别垂直AB，BC于点D、E，若 $A D = 3$ ， $C E = 4$ ，则 $⊙ O$ 的半径长为．

查看试题解析
13. a、b、c是实数，点A（a－1、b）、B（a－2，c）在二次函数y＝x²－2ax＋1的图像上，
则b、c的大小关系是：bc（用“＞”或“＜”号填空）．

查看试题解析
14. 如图所示， $△ A B C$ 是边长为9cm的等边三角形，被一平行于BC的矩形所截，AB被截成三等分，则图中阴影部分的面积为 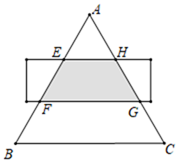$c m^{2}$ ．

查看试题解析
15. 如图，在平面直角坐标系xOy中，已知抛物线 $y = \frac{3}{8} x^{2} - \frac{3}{4} x - 3$ 与x轴交于点A、 $B (A$ 在B左侧 $)$ ，与y轴交于点C，经过点A的射线AF与y轴正半轴相交于点E，与抛物线的另一个交点为F， $\frac{A E}{E F} = \frac{1}{3}$ ，点D是点C关于抛物线对称轴的对称点，点P是y轴上一点，且 $∠ A F P = ∠ D A B$ ，则点P的坐标是．

查看试题解析
16. 已知：如图，在 $△ A B C$ 中，点D在BC上，点E在AC上，DE与AB不平行 $.$ 添加一个条件，使得 $△ C D E$ ∽ $△ C A B$ ，然后再加以证明．

查看试题解析

三、解答题

17. 一只箱子里共有3个球，其中2个白球，1个红球，它们除颜色外均相同。

(1)、从箱子中任意摸出一个球是白球的概率是多少？

(2)、从箱子中任意摸出一个球，不将它放回箱子，搅匀后再摸出一个球，求两次摸出球的都是白球的概率，并画出树状图。

查看试题解析
18. 如图，某消防队在一居民楼前进行演习，消防员利用云梯成功救出点B处的求救者后，又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°，点A距地面2.5米，点B距地面10.5米.为救出点C处的求救者，云梯需要继续上升的高度BC约为多少米？（结果保留整数.参考数据：tan65°≈2.1，sin65°≈0.9，cos65°≈0.4， $\sqrt{2}$ ≈1.4）

查看试题解析
19. 如图，正方形ABC的顶点A在抛物线y＝x²上，顶点B ， C在x轴的正半轴上，且点B的坐标为（1，0）

(1)、求点D坐标；

(2)、将抛物线y＝x²适当平移，使得平移后的抛物线同时经过点B与点D ，求平移后抛物线解析式，并说明你是如何平移的．

查看试题解析
20. 如图， $∠ M A N = 30^{\circ}$ ，点O为边AN上一点，以O为圆心，6为半径作 $⊙ O$ 交AN于D、E两点．

(1)、当 $⊙ O$ 与AM相切时，求AD的长；

(2)、如果 $A D = 3$ ，判断AM与 $⊙ O$ 的位置关系？并说明理由．

查看试题解析
21. 已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B（点A在点B左侧），根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”．

(1)、①如图2，求出抛物线 $y = x^{2}$ 的“完美三角形”斜边AB的长；
②抛物线 $y = x^{2} + 1$ 与 $y = x^{2}$ 的“完美三角形”的斜边长的数量关系是；

(2)、若抛物线 $y = a x^{2} + 4$ 的“完美三角形”的斜边长为4，求a的值；

(3)、若抛物线 $y = m x^{2} + 2 x +n - 5$ 的“完美三角形”斜边长为n，且 $y = m x^{2} + 2 x +n - 5$ 的最大值为-1，求m，n的值．

查看试题解析
22. 如图，半径为4且以坐标原点为圆心的圆O交x轴，y轴于点B、D、A、C，过圆上的动点 $P ($ 不与A重合 $)$ 作 $P E ⊥ P A$ ，且 $P E = P A (E$ 在AP右侧 $)$ ．

(1)、当P与C重合时，求出E点坐标；

(2)、连接PC，当 $P C = 5$ 时，求点P的坐标；

(3)、连接OE，直接写出线段OE的取值范围．

查看试题解析