陕西省渭南市临渭区2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
2. 已知反比例函数y= $\frac{k}{x}$ 的图象经过点P（﹣2，3），则下列各点也在这个函数图象的是（）

A、（﹣1，﹣6） B、（1，6） C、（3，﹣2） D、（3，2）

查看试题解析
3. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，则符合这一结果的实验最有可能的是（　　）
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333

A、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 B、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” C、抛一个质地均匀的正六面体骰子，向上的面点数是5 D、抛一枚硬币，出现反面的概率

查看试题解析
4. 菱形，矩形，正方形都具有的性质是（　　）

A、对角线相等且互相平分 B、对角线相等且互相垂直平分 C、对角线互相平分 D、四条边相等，四个角相等

查看试题解析
5. 若2- $\sqrt{3}$ 是方程x²-4x+c=0的一个根，则c的值是（）

A、1 B、3- $\sqrt{3}$ C、1+ $\sqrt{3}$ D、2+ $\sqrt{3}$

查看试题解析
6. 已知 $P_{1} (x_{1}, y_{1})$ ， $∠ A =$ ， $P_{3} (x_{3}, y_{3})$ 是反比例函数 $y = \frac{6}{x}$ 的图像上三点，且 $y_{1} < y_{2} < 0 < y_{3}$ ，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{3} < x_{2} < x_{1}$ C、 $x_{2} < x_{1} < x_{3}$ D、 $x_{2} < x_{3} < x_{1}$

查看试题解析
7. 如图，点 $M$ 是平行四边形 $A B C D$ 边 $C D$ 上的一点， $B M$ 的延长线交 $A D$ 的延长线于点 $N$ ，则图中相似的三角形有（）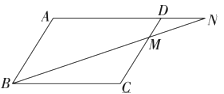

A、3对 B、2对 C、1对 D、0对

查看试题解析
8. 在一个不透明的袋子里装有两个黄球和一个白球，它们除颜色外都相同，随机从中摸出一个球，记下颜色后放回袋子中，充分摇匀后，再随机摸出一个球．两次都摸到黄球的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{1}{3}$ C、 $\frac{2}{9}$ D、 $\frac{1}{9}$

查看试题解析
9. 某市决定改善城市容貌，绿化环境，计划经过两年时间，绿地面积增加 $44 %$ ，这两年平均每年绿地面积的增长率是（）

A、 $20 %$ B、 $11 %$ C、 $22 %$ D、 $44 %$

查看试题解析
10. 如图正方形ABCD中，点E、F分别在CD、BC边上，△AEF是等边三角形．以下结论：①EC＝FC；②∠AED＝75°；③AF＝ $\sqrt{2}$ CE；④EF的垂直平分线是直线AC．正确结论个数有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 若关于x的一元二次方程kx²﹣2x+1＝0有实数根，则k的取值范围是．

查看试题解析
12. 如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的
位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF离地面的高度AC=1.5 m，CD=8 m，则树高AB= ．

查看试题解析
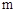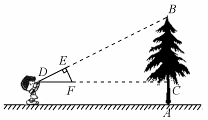13. 如图，已知正方形ABCD的边长为5，点E、F分别在AD、DC上，AE=DF=2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为．

查看试题解析

三、解答题

14. 解方程： $x^{2} - 4 = 3 (x + 2)$

查看试题解析
15. 从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件.

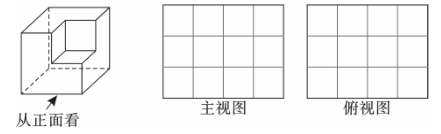(1)、这个零件的表面积是；

(2)、请在边长为1的网格图里画出这个零件的主视图和俯视图.

查看试题解析
16. 已知方程ax²+bx+c=0（a≠0）是关于x的一元二次方程．

(1)、直接写出方程根的判别式；

(2)、写出求根公式的推导过程．

查看试题解析
17. 如图，在11×14的网格图中，△ABC三个顶点坐标分别为A（﹣4，1），B（﹣1，1），（﹣2，4）．

(1)、以A为位似中心，将△ABC放大为原来的2倍得到△AB₁C₁ ，请在网格图画出△AB₁C₁；

(2)、直接写出（1）中点B₁ ， C₁的坐标．

查看试题解析
18. 如图，在菱形 $A B C D$ 中， $D E ⊥ A B$ ，垂足为点 $E$ ，且 $E$ 为边 $A B$ 的中点.

(1)、求 $∠ A$ 的度数；

(2)、如果 $A B = 4$ ，求对角线 $A C$ 的长.

查看试题解析
19. 如图，在平面直角坐标系中，平行四边形 $A B C D$ 的边 $A B = 2$ ，顶点 $A$ 坐标为 $（ 1 ， b)$ ，点 $D$ 坐标为 $(2 ， b + 1)$ .

(1)、点 $B$ 的坐标是，点 $C$ 的坐标是（用 $b$ 表示）；

(2)、若双曲线 $y = \frac{k}{x}$ 过平行四边形 $A B C D$ 的顶点 $B$ 和 $D$ ，求该双曲线的表达式；

(3)、若平行四边形 $A B C D$ 与双曲线 $y = \frac{4}{x} (x > 0)$ 总有公共点，求 $b$ 的取值范围.

查看试题解析
20. 为进一步深化基教育课程改革，构建符合素质教育要求的学校课程体系，某学校自主开发了A书法、B阅读，C足球，D器乐四门校本选修课程供学生选择，每门课程被选到的机会均等．

(1)、学生小红计划选修两门课程，请写出所有可能的选法；

(2)、若学生小明和小刚各计划送修一门课程，则他们两人恰好选修同一门课程的概率为多少？

查看试题解析
21. 在一次关于相似三角形的探究活动中，如图所示： $∠ A C B = ∠ A D E$ ，老师让大家适当的添上辅助线，看看还能得到哪些相似三角形，小颖连接 $C D$ 、 $B E$ ，且 $C D$ 、 $B E$ 相交于点 $F$ ，于是她得到了 $Δ A C D ∽ Δ A B E$ .下面是她的证明过程的一部分，你能帮助她完成证明吗？

(1)、证明：∵ $∠ A = ∠ A$ ， $∠ A C B = ∠ A D E$
∴ $Δ A C B ∽ Δ A D E$

∴ $\frac{A C}{A D} =$

又∵

∴ $Δ A C D ∽ A B E$

(2)、你还能得到图中哪些三角形是相似的？至少写出两对.

查看试题解析
22. 列方程解应用题：
某玩具厂生产一种玩具，按照控制固定成本降价促销的原则，使生产的玩具能够及时售出，据市场调查：每个玩具按480元销售时，每天可销售160个；若销售单价每降低1元，每天可多售出2个．已知每个玩具的固定成本为360元，设这种玩具的销售单价为x元．

(1)、根据销售单价每降低1元，每天可多售出2个，则现在销售数量为个（用含有x的代数式表示）

(2)、当x为多少元时，厂家每天可获利润20000元？

查看试题解析
23. 在一次数学活动课上，李老师带领学生去测量教学楼的高度．在阳光下，测得身高1.65m的黄丽同学BC的影子BA长1.1m，与此同时，测得教学楼DE的影子DF长12.1m.

(1)、请你在图中画出此时教学楼DE在阳光下的影子DF；

(2)、请你根据已测得的数据，求出教学楼DE的高度(精确到0.1m)．

查看试题解析
24. 如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．

(1)、求证：四边形CEDF是平行四边形；

(2)、①当AE=cm时，四边形CEDF是矩形；
②当AE=cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）

查看试题解析

实验次数	100	200	300	500	800	1000	2000
频率	0.365	0.328	0.330	0.334	0.336	0.332	0.333