广西来宾市2019届九年级上学期期末教学质量调研数学试卷
试卷更新日期:2019-12-16 类型:期末考试
一、单选题
-
1. 下列各点中,在函数y=- 图象上的是( )A、 B、 C、 D、2. 在Rt△ABC中,∠C=90°,如果AB=2,BC=1,那么sinA的值是( )A、 B、 C、 D、3. 某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验,得到两个品种每公顷产量的两组数据,其方差分别为s甲2=0.002、s乙2=0.03,则 ( )
A、甲比乙的产量稳定 B、乙比甲的产量稳定 C、甲、乙的产量一样稳定 D、无法确定哪一品种的产量更稳定4. 下列一元二次方程中,有两个相等的实数根的是( )A、 B、 C、 D、5. 如图,在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( )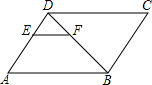 A、 B、8 C、10 D、166. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
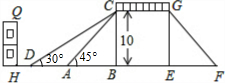
A、 B、8 C、10 D、166. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )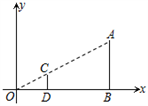 A、(2,1) B、(2,0) C、(3,3) D、(3,1)7. 已知反比例函数y= , 下列结论中不正确的是 ( )A、图象经过点(-1,-1) B、图象在第一、三象限 C、当x>1时,0<y<1 D、当x<0时,y随着x的增大而增大8. 若方程x2-3x-1=0的两根为x1、x2 , 则 + 的值为( )A、3 B、-3 C、 D、-9. 如果△ABC∽△DEF , A、B分别对应D、E , 且AB∶DE=1∶2,那么下列等式一定成立的是( )A、BC∶DE=1∶2 B、△ABC的面积∶△DEF的面积=1∶2 C、∠A的度数∶∠D的度数=1∶2 D、△ABC的周长∶△DEF的周长=1∶210. 在一幅长8分米,宽6分米的矩形风景画(如图甲)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图乙),使整个挂图的面积是80平方分米,设金色纸边的宽度为x分米,则可列方程为( )
A、(2,1) B、(2,0) C、(3,3) D、(3,1)7. 已知反比例函数y= , 下列结论中不正确的是 ( )A、图象经过点(-1,-1) B、图象在第一、三象限 C、当x>1时,0<y<1 D、当x<0时,y随着x的增大而增大8. 若方程x2-3x-1=0的两根为x1、x2 , 则 + 的值为( )A、3 B、-3 C、 D、-9. 如果△ABC∽△DEF , A、B分别对应D、E , 且AB∶DE=1∶2,那么下列等式一定成立的是( )A、BC∶DE=1∶2 B、△ABC的面积∶△DEF的面积=1∶2 C、∠A的度数∶∠D的度数=1∶2 D、△ABC的周长∶△DEF的周长=1∶210. 在一幅长8分米,宽6分米的矩形风景画(如图甲)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图乙),使整个挂图的面积是80平方分米,设金色纸边的宽度为x分米,则可列方程为( ) A、 B、 C、 D、11. 如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A、 B、 C、 D、11. 如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )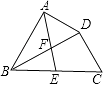 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
12. 将方程2x2=1-3x化为一般形式是 .13. 如果两个相似三角形的面积比是1:9,那么这两个三角形的相似比是 .14. 某商品原售价300元,经过连续两次降价后售价为260元,设平均每次降价的百分率为x,则满足x的方程是 .15. 已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为米.16. 从某校参加毕业考的学生中,随机抽查了20名学生的数学成绩,分数如下:
90
84
88
86
98
78
61
54
100
97
95
84
70
71
77
85
72
63
79
48
可以估计该校这次参加毕业会考的数学平均成绩为 .
17. 如图,等边三角形OAB的一边OA在x轴上,双曲线y= 在第一象限内的图象经过OB边的中点C,则点B的坐标是 .
三、解答题
-
18. 解方程:x2﹣4x+1=019. 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分)
频数(人)
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25
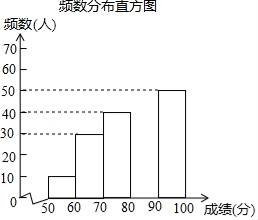
根据所给信息,解答下列问题:
(1)、m= , n=;(2)、补全频数分布直方图;(3)、这200名学生成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?20. 如图, 在方格纸中.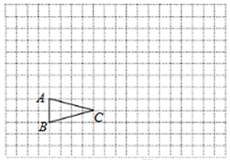 (1)、请在方格纸上建立平面直角坐标系,使 , ,并求出 点坐标;(2)、以原点 为位似中心,相似比为2,在第一象限内将 放大,画出放大后的图形
(1)、请在方格纸上建立平面直角坐标系,使 , ,并求出 点坐标;(2)、以原点 为位似中心,相似比为2,在第一象限内将 放大,画出放大后的图形 ; (3)、计算
; (3)、计算 的面积 . 21. 已知一元二次方程x2-4x+k=0有两个不相等的实数根.(1)、求k的取值范围;(2)、如果一元二次方程x2-4x+k=0有一个根是3,求另一个根和k的值.22. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?23. 如图,一次函数y=kx+b与反比例函数y=
的面积 . 21. 已知一元二次方程x2-4x+k=0有两个不相等的实数根.(1)、求k的取值范围;(2)、如果一元二次方程x2-4x+k=0有一个根是3,求另一个根和k的值.22. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?23. 如图,一次函数y=kx+b与反比例函数y=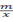 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点. 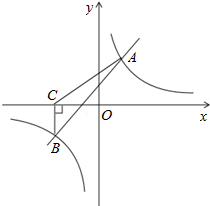 (1)、求一次函数与反比例函数的解析式;(2)、根据所给条件,请直接写出不等式kx+b> 的解集;(3)、过点B作BC⊥x轴,垂足为C,求S△ABC .
(1)、求一次函数与反比例函数的解析式;(2)、根据所给条件,请直接写出不等式kx+b> 的解集;(3)、过点B作BC⊥x轴,垂足为C,求S△ABC .