重庆市綦江区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2019-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. $- 2$ 的相反数是（）

A、2 B、 $- 2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列运算正确的是（）

A、﹣（﹣2）＝﹣2 B、|﹣3|＝﹣3 C、﹣2²＝4 D、（﹣3）÷（﹣ $\frac{1}{3}$ ）＝9

查看试题解析
3. 若 $a$ 、 $b$ 互为相反数， $c$ 、 $d$ 互为倒数， $m$ 的绝对值为2，则 $m • m^{} - c d + \frac{a + b}{m}$ 值为（）

A、 $- 3$ B、3 C、 $- 5$ D、3或 $- 5$

查看试题解析
4. 已知a ， b在数轴上的位置如图所示，那么下面结论正确的是（）

A、a﹣b＜0 B、ab＞0 C、a+b＜0 D、|a|＞|b|

查看试题解析
5. 下列说法中正确的个数为（）
⑴过两点有且只有一条直线；⑵连接两点的线段叫两点间的距离；⑶两点之间所有连线中，线段最短；⑷射线比直线小一半．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 若a﹣b＝﹣2，ab＝3，则代数式3a+2ab﹣3b的值为（）

A、12 B、0 C、﹣12 D、﹣8

查看试题解析
7. 我国倡导的“一带一路”地区覆盖的总人口为4400000000人，这个数用科学记数法表示为（）

A、44×10⁸ B、4.4×10⁸ C、4.4×10⁹ D、44×10¹⁰

查看试题解析
8. 如图是正方体的平面展开图，每个面上都标有一个汉字，与“爱”字对应的面上的字为（）

A、大 B、美 C、綦 D、江

查看试题解析
9. 2018年4月12日我军在南海举行了建国以来海上最大的军事演习，位于点O处的军演指挥部观测到军舰A位于点O的北偏东70°方向（如图），同时观测到军舰B位于点O处的南偏西15°方向，那么∠AOB的大小是（）

A、85° B、105° C、115° D、125°

查看试题解析
10. 某班组每天需生产50个零件才能在规定的时间内完成一批零件任务，实际上该班组每天比计划多生产了6个零件，结果比规定的时间提前3天并超额生产120个零件，若设该班组要完成的零件任务为x个，则可列方程为（）

A、 $\frac{x + 120}{50} - \frac{x}{50 + 6} = 3$ B、 $\frac{x}{50} - \frac{x}{50 + 6} = 3$ C、 $\frac{x}{50} - \frac{x + 120}{50 + 6} = 3$ D、 $\frac{x + 120}{50 + 6} - \frac{x}{50} = 3$

查看试题解析
11.
按下面的程序计算：

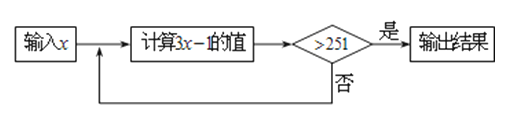
当输入x=100时，输出结果是299；当输入x=50时，输出结果是446；如果输入x的值是正整数，输出结果是257，那么满足条件的x的值最多有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图①是一块瓷砖的图案，用这种瓷砖来铺设地面，如果铺成一个2×2的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个3×3的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个4×4的正方形图案（如图④），其中完整的圆共有25个，若这样铺成一个10×10的正方形图案，则其中完整的圆共有（）个.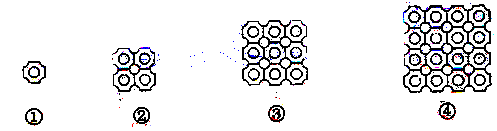

A、145 B、146 C、180 D、181

查看试题解析

二、填空题

13. 綦江某天白天气温最高为+11℃，夜间最低为﹣2℃，则綦江当天的最大温差为℃．

查看试题解析
14. 若3x^m⁺⁵y与x³y是同类项，则m= ．

查看试题解析
15. 若|3m﹣5|+（n+3）²＝0，则6m﹣（n+2）＝．

查看试题解析
16. 如图是六个棱长为1的立方块组成的一个几何体，其俯视图的面积是．

查看试题解析
17. 现在规定一种新运算：对于任意实数对（a ， b），满足a※b＝a²﹣b﹣5，若45※m＝1，则m＝．

查看试题解析
18. 某服装厂生产某种冬装，9月份销售每件冬装的利润是出厂价的25%（每件冬装的利润＝出厂价﹣成本），10份将每件冬装的出厂价降低10%，（每件冬装的成本不变），销售量则比9月份增加80%，那么该厂10份销售这种冬装的利润总额比9月的利润总额增长%．

查看试题解析

三、解答题

19. 计算：

(1)、（﹣3）²﹣6× $\frac{1}{3}$ ÷（﹣2）

(2)、﹣1⁴﹣24× $(\frac{5}{8} - \frac{3}{4})$ ﹣|﹣5|

查看试题解析
20. 解方程：

(1)、4﹣3（8﹣x）＝5（x﹣2）

(2)、 $\frac{y + 2}{4}$ ﹣ $\frac{2 y - 1}{6}$ ＝1

查看试题解析
21. 先化简，再求值：2ab（b﹣2a）﹣3ab（b﹣2a），其中a＝﹣2，b＝1．

查看试题解析
22. 出租车司机小王某天下午2：00～4：00的营运全是在东西走向的大道上进行的，如果规定向东行驶为正，他这天下午行车的里程（单位：千米）如下：+5，﹣13，+7，﹣11，+16，﹣8，﹣3．

(1)、若把小王下午2：00的出发地记为0，他4：00将最后一名乘客送到目的地时，距下午出发地有多远？

(2)、小王离下午出发地最远时是多少千米？

(3)、若每千米的营运额为5元，小王这天下午2：00～4：00的营业额为多少？

查看试题解析
23. 如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°.

(1)、请你数一数，图中有多少个小于平角的角；

(2)、求出∠BOD的度数；

(3)、请通过计算说明OE是否平分∠BOC．

查看试题解析
24. 某商场推出新年大促销活动，其中标价为300元的某种商品打8折出售，这时商品的利润率仍有20%.

(1)、求该商品的成本价是多少？

(2)、该商品在降价前一周的销售额达到了12000元，要使该商品降价后一周内的销售额也要达到12000元，降价后一周内的销售数量应该比降价前一周内的销售数量增加m%，求m的值．

查看试题解析

25. 为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：

每月用气量	单价（元/m³）
不超出75m³的部分	2.5
超出75m³不超出125m³的部分	a
超出125m³的部分	a+0.25

(1)、若甲用户3月份的用气125m³ ，缴费325元，求a的值；

(2)、在（1）的条件下，若乙用户2、3月份共用气175m³（3月份用气量低于2月份用气量），共缴费455元，乙用户2、3月份的用气量各是多少？

查看试题解析

26. 如图，已知点A、B、C是数轴上三点，O为原点．点C对应的数为6，BC＝4，AB＝12．

(1)、求点A、B对应的数；

(2)、动点P、Q分别同时从A、C出发，分别以每秒6个单位和3个单位的速度沿数轴正方向运动．M为AP的中点，N在CQ上，且CN＝ $\frac{1}{3}$ CQ ，设运动时间为t（t＞0）．
①求点M、N对应的数（用含t的式子表示）； ②t为何值时，OM＝2BN ．

查看试题解析