重庆市梁平区2018-2019学年七年级上学期期末考试数学试题

试卷更新日期：2019-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $- (- 3) = - 3$ B、 $- | - 3 | = - 3$ C、 $- (+ 3) = 3$ D、 $- | - 3 | = 3$

查看试题解析
2. 下列运算正确的是（）

A、 $- 3 (x - 1) = - 3 x - 1$ B、 $- 3 (x - 1) = - 3 x + 1$ C、 $- 3 (x - 1) = - 3 x - 3$ D、 $- 3 (x - 1) = - 3 x + 3$

查看试题解析
3. 图中 $∠ 1$ 和 $∠ 2$ 是对顶角的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各组数中，数值相等的是（）

A、 $- 2^{3}$ 和 ${(- 2)}^{3}$ B、 $- 2^{2}$ 和 ${(- 2)}^{2}$ C、 $- 2^{3}$ 和 $- 3^{2}$ D、 $- 1^{10}$ 和 ${(- 1)}^{10}$

查看试题解析
5. 港珠澳大桥是连接香港、珠海、澳门的超大型跨海通道，全长约55000米，把55000用科学记数法表示为（）

A、55×10³ B、5.5×10⁴ C、5.5×10⁵ D、0.55×10⁵

查看试题解析
6. 从正面观察如图所示的两个物体，看到的主视图是（）

A、 B、 C、 D、

查看试题解析
7. 在数学课上，同学们在练习过点B作线段AC所在直线的垂线段时，有一部分同学画出下列四种图形，请你数一数，错误的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知2y-x=5，那么 $5 {(x - 2 y)}^{2} - 3 x + 6 y - 60$ 的值为（）

A、10 B、40 C、80 D、210

查看试题解析
9. 日常生活中我们使用的数是十进制数 $.$ 而计算机使用的数是二进制数，即数的进位方法是“逢二进一” $.$ 二进制数只使用数字0，1，如二进制数1101记为 $1101_{2}$ ， $1101_{2}$ 通过式子 $1 \times 2^{3} + 1 \times 2^{2} + 0 \times 2 + 1$ 可以转换为十进制数13，仿照上面的转换方法，将二进制数 $11101_{2}$ 转换为十进制数是（）

A、4 B、25 C、29 D、33

查看试题解析
10. 如图所示，第1个图案是由黑白两种颜色的六边形地面砖组成的，第2个，第3个图案可以看成是由第1个图案经过平移而得，那么第n个图案中有白色六边形地面砖（）块．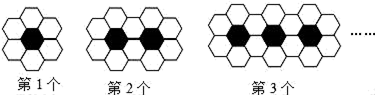

A、6+4（n+1） B、6+4n C、4n﹣2 D、4n+2

查看试题解析
11. 若“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1，…，则 $\frac{100!}{98!}$ 的值为（）

A、 $\frac{50}{49}$ B、99! C、9900 D、2！

查看试题解析

二、填空题

12. 单项式 $－ \frac{2 x^{2} y}{3}$ 的系数是。

查看试题解析
13. 将多项式 $2 x^{3} y - 4 y^{2} + 3 x^{2} - x$ 按 $x$ 的降幂排列为．

查看试题解析
14. 若 ${(x - 2)}^{2} + | y + \frac{1}{3} | = 0$ ，则 $y^{x} =$ ．

查看试题解析
15. 如图，已知AE∥BD ， ∠1＝130°，∠2＝30°，则∠C＝度．

查看试题解析
16. 若 $| a | = 5$ ， $| b | = 3$ ，且 $a + b < 0$ ，那么 $a - b =$ ．

查看试题解析
17. 数学家发明了一个魔术盒，当任意数对 $(a ， b)$ 放入其中时，会得到一个新的数： $a {}^{2}+ b + 1$ ．例如把 $(3 ， - 2)$ 放入其中，就会得到 $3^{2} + (- 2) + 1 = 8$ ．现将数对 $(- 2 ， 3)$ 放入其中得到数m= ，再将数对 $(m ， 1)$ 放入其中后，得到的数是．

查看试题解析

三、解答题

18. 计算：

(1)、 $- 1^{3} - (1 + 0.5) \times \frac{1}{3} \div (- 4)$

(2)、 $- 3.375 \times 12 + 4.375 \div \frac{1}{12} - 36 \times (\frac{1}{18} - \frac{1}{12} + \frac{1}{3})$

(3)、 $6 \frac{1}{2} \times {(- 2)}^{4} \div [{(- 2)}^{3} - (- 2)^{2} - 2^{2}] \div (- \frac{4}{3})$

查看试题解析
19. 先化简，再求值．

(1)、 $5 x^{2} - (3 y^{2} + 5 x^{2}) + (4 y^{2} + 7 xy)$ ，其中 $x = - 1$ ， $y = 1$ ．

(2)、 $\frac{1}{3} x^{2} - (3 x^{2} + 3 xy - \frac{3}{5} y^{2}) + (\frac{8}{3} x^{2} + 3 xy + \frac{2}{5} y^{2})$ ，其中 $x = \frac{1}{2}$ ， $y = 2$ ．

查看试题解析

20. 自从我们有了用字母表示数，发现表达有关的数和数量关系更加简洁明了，从而有助于我们发现更多有趣的结论，请你按要求试一试

(1)、完善表格．

	a与b和的平方	a、b两数平方的和与a、b两数积的2倍的和
用代数式表示		$a^{2} + b^{2} + 2 ab$
$a = 3$ ， $b = - 2$		1
$a = - 4$ ， $b = 1$
$a = - 6$ ， $b = - 2$

根据表中计算结果，你发现了什么等式？

(2)、利用

(1)

中发现的结论，计算

2001^{2} + 1992^{2} - 2 \times 2001 \times 1999

查看试题解析

21. 某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信，这五封信的重量分别是

72 g ， 90 g ， 215 g ， 340 g ， 400 g

.根据这五所学校的地址及信件的重量范围，在邮局查得相关邮费标准如下：

业务种类	计费单位	资费标准/元	挂号费/（元/封）	特制信封（元/个）
挂号信	首重100g，每重20g	0.8	3	0.5
挂号信	续重101~2000g，每重100g	2.00	3	0.5
特制信封	首重1000g内	5.00	3	1.0

(1)、重量为90g的信若以“挂号信”方式寄出，邮寄费为多少元？若以“特快专递”方式寄出呢？

(2)、这五封信分别以怎样的方式寄出最合算？请说明理由.

(3)、通过解答上述问题，你有何启示？（请你用一两句话说明）

查看试题解析

22. 体育课上，全班男同学进行了100米测验，达标成绩为15秒，下表是某小组8名男生的成绩记录，其中“+”表示成绩大于15秒．

﹣0.87

+1

﹣1.2

0

﹣0.7

+0.6

﹣0.4

﹣0.1

问：

(1)、这个小组男生的达标率为多少？

(2)、这个小组男生的平均成绩是多少秒？

查看试题解析
23. 已知：如图，B、C是线段AD上两点，且AB：BC： $CD = 2$ ：4：3，M是AD的中点， $BM = 15 cm$ ，求线段MC的长．

查看试题解析
24. 问题情景：如图1， $AB / / CD$ ， $∠ PAB = 130^{\circ}$ ， $∠ PCD = 120^{\circ}$ ，求 $∠ APC$ 的度数．

(1)、天天同学看过图形后立即口答出： $∠ APC = 110^{\circ}$ ，请你补全他的推理依据．
如图2，过点P作 $PE / / AB$ ，

$∵ AB / / CD$ ，

$∴ PE / / AB / / CD . ($ $)$

$∴ ∠ A + ∠ APE = 180^{\circ}$ ．

$∠ C + ∠ CPE = 180^{\circ} . ($ $)$

$∵ ∠ PAB = 130^{\circ}$ ， $∠ PCD = 120^{\circ}$ ，

$∴ ∠ APE = 50^{\circ}$ ， $∠ CPE = 60^{\circ}$

$∴ ∠ APC = ∠ APE + ∠ CPE = 110^{\circ} . ($ $)$

问题迁移：

(2)、如图3， $AD / / BC$ ，当点P在A、B两点之间运动时， $∠ ADP = ∠ α$ ， $∠ BCP = ∠ β$ ，求 $∠ CPD$ 与 $∠ α$ 、 $∠ β$ 之间有何数量关系？请说明理由．

(3)、在（2）的条件下，如果点P在A、B两点外侧运动时 $($ 点P与点A、B、O三点不重合 $)$ ，请你直接写出 $∠ CPD$ 与 $∠ α$ 、 $∠ β$ 之间的数量关系．

查看试题解析