吉林省长春市德惠市九校2019-2020学年高二上学期理数期中考试试卷

试卷更新日期：2019-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 命题“若 $a < b$ ，则 $a + c < b + c$ ”的逆否命题是

A、若 $a + c < b + c$ ，则 $a > b$ B、若 $a + c > b + c$ ，则 $a > b$ C、若 $a + c < b + c$ ，则 $a \geq b$ D、若 $a + c \geq b + c$ ，则 $a \geq b$

查看试题解析
2. 对于命题 $p$ 和 $q$ ，若 $p$ 且 $q$ 为真命题，则下列四个命题：① $p$ 或 $\neg q$ 是真命题，② $p$ 且 $\neg q$ 是真命题，③ $\neg p$ 且 $q$ 是假命题，④ $\neg p$ 或 $q$ 是假命题，其中真命题是（）

A、①② B、③④ C、②④ D、①③

查看试题解析
3. 已知 $\vec{a} = (2, - 3, 1)$ ， $\vec{b} = (4, - 6, x)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $x$ 等于（）

A、-26 B、-10 C、2 D、10

查看试题解析
4. 以下四组向量中，互相平行的有（）组.
⑴ $\vec{a} = (1, 2, 1)$ , $\vec{b} = (1, - 2, 3)$ ； ⑵ $\vec{a} = (8, 4, - 6)$ , $\vec{b} = (4, 2, - 3)$ ；

⑶ $\vec{a} = (0, 1, - 1)$ , $\vec{b} = (0, - 3, 3)$ ； ⑷ $\vec{a} = (- 3, 2, 0)$ , $\vec{b} = (4, - 3, 3)$

A、一组 B、二组 C、三组 D、四组

查看试题解析
5. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = A D = 1$ ， $A A_{1} = 2$ 则异面直线 $A_{1} B_{1}$ 与 $A C_{1}$ 所成角的正切值为（）

A、 $\sqrt{5}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6. 对抛物线 $y = 4 x^{2}$ ，下列描述正确的是（）

A、开口向上，焦点为 $(0, 1)$ B、开口向上，焦点为 $(0, \frac{1}{16})$ C、开口向右，焦点为 $(1, 0)$ D、开口向右，焦点为 $(0, \frac{1}{16})$

查看试题解析
7. 以 $F (0, \frac{p}{2})$ $(p > 0)$ 为焦点的抛物线 $C$ 的准线与双曲线 $x^{2} - y^{2} = 2$ 相交于 $M, N$ 两点，若 $△ M N F$ 为正三角形，则抛物线 $C$ 的标准方程为（）

A、 $y^{2} = 2 \sqrt{6} x$ B、 $y^{2} = 4 \sqrt{6} x$ C、 $x^{2} = 4 \sqrt{6} y$ D、 $x^{2} = 2 \sqrt{6} y$

查看试题解析
8. 若焦点在x轴上的椭圆 $\frac{x^{2}}{2} + \frac{y^{2}}{n} = 1$ 的离心率为 $\frac{1}{2}$ ，则n=( )

A、 $\sqrt{3}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、 $\frac{8}{3}$

查看试题解析
9. 已知点P是抛物线x= $\frac{1}{4}$ y²上的一个动点，则点P到点A（0，2）的距离与点P到y轴的距离之和的最小值为（）

A、2 B、 $\sqrt{5}$ C、 $\sqrt{5}$ ﹣1 D、 $\sqrt{5}$ +1

查看试题解析
10. “k＞9”是“方程 $\frac{x^{2}}{9 - k} + \frac{y^{2}}{k - 4} = 1$ 表示双曲线”的（）

A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件

查看试题解析
11. 如图所示，在长方体ABCDA₁B₁C₁D₁中，AD＝AA₁＝1，AB＝2，点E是棱AB的中点，则点E到平面ACD₁的距离为（）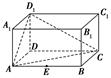

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
12. 已知椭圆C的方程为 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，焦距为 $2 c$ ，直线 $l : y = \frac{\sqrt{2}}{4} x$ 与椭圆C相交于A，B两点，若 $| A B | = 2 c$ ，则椭圆C的离心率为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析

二、填空题

13. 直角坐标平面 $x O y$ 中，若定点 $A (1, 2)$ 与动点 $P (x, y)$ 满足 $\vec{O P} \cdot \vec{O A} = 4$ ，则点 $P$ 的轨迹方程是

查看试题解析
14. 已知曲线 $x^{2} - 4 y^{2} = 4$ ，过点 $A (3, 1)$ 且被点 $A$ 平分的弦 $M N$ 所在的直线方程为.

查看试题解析
15. 给出下列命题：
①命题“若 $x^{2} = 1$ ，则 $x = 1$ ”的否命题为“若 $x^{2} = 1$ ，则 $x \neq 1$ ”；

②“ $x = - 1$ ”是“ $x^{2} - 5 x - 6 = 0$ ”的必要不充分条件；

③ $\exists x \in R$ 命题“，使得 $x^{2} + x - 1 < 0$ ”的否定是：“ $\forall x \in R$ ，均有 $x^{2} - x - 1 > 0$ ”；

④命题“若 $x = y$ ，则 $\sin x = \sin y$ ”的逆否命题为真命题

其中所有正确命题的序号是.

查看试题解析
16. 已知 $F_{1}, F_{2}$ 分别为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的左、右焦点，过 $F_{2}$ 与双曲线的一条渐近线平行的直线交双曲线于点 $P$ ，若 $| P F_{1} | = 3 | P F_{2} |$ ，则双曲线的离心率为.

查看试题解析

三、解答题

17. 已知 $p :$ 实数 $x$ ，满足 $x - a < 0$ ， $q :$ 实数 $x$ ，满足 $x^{2} - 4 x + 3 \leq 0$ .

(1)、若 $a = 2$ 时 $p \land q$ 为真，求实数 $x$ 的取值范围；

(2)、若 $p$ 是 $q$ 的必要不充分条件，求实数 $a$ 的取值范围

查看试题解析
18. 已知抛物线 $C$ ： $x^{2} = 2 p y (p > 0)$ 的焦点为 $F$ ，点 $P (x_{0}, 3)$ 为抛物线 $C$ 上一点，且点 $P$ 到焦点 $F$ 的距离为4，过 $A (a, 0)$ 作抛物线 $C$ 的切线 $A N$ （斜率不为0），切点为 $N$ .
（Ⅰ）求抛物线 $C$ 的标准方程；

（Ⅱ）求证：以 $F N$ 为直径的圆过点 $A$ .

查看试题解析
19. 如图，四棱锥 $P - A B C D$ 中， $PD ⊥$ 平面 $A B C D$ ，底面 $A B C D$ 是正方形 $P D = A B = 2$ ， $E$ 为 $P C$ 中点.

(1)、求证： $D E ⊥$ 平面 $P C B$ ；

(2)、求点 $C$ 到平面 $D E B$ 的距离；

(3)、求二面角 $E - B D - P$ 的余弦值.

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的两个焦点分别为F₁ ， F₂ ，离心率为 $\frac{1}{2}$ ，过F₁的直线l与椭圆C交于M ， N两点，且△MNF₂的周长为8．

(1)、求椭圆C的方程；

(2)、若直线y＝kx＋b与椭圆C分别交于A ， B两点，且OA⊥OB ，试问点O到直线AB的距离是否为定值，证明你的结论．

查看试题解析
21. 设A ， B分别为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ (a>0，b>0)的左、右顶点，双曲线的实轴长为4 $\sqrt{3}$ ，焦点到渐近线的距离为 $\sqrt{3}$ .

(1)、求双曲线的方程；

(2)、已知直线y＝ $\frac{\sqrt{3}}{3}$ x－2与双曲线的右支交于M ， N两点，且在双曲线的右支上存在点D ，使 $\vec{O M} + \vec{O N} = t \vec{O D}$ ，求t的值及点D的坐标．

查看试题解析
22. 已知点 $C$ 为圆 ${(x + 1)}^{2} + y^{2} = 8$ 的圆心， $P$ 是圆上的动点，点 $Q$ 在圆的半径 $C P$ 上，且有点 $A (1, 0)$ 和 $A P$ 上的点 $M$ ，满足 $\vec{M Q} \cdot \vec{A P} = 0, \vec{A P} = 2 \vec{A M}$ .
(Ⅰ)当点 $P$ 在圆上运动时，判断 $Q$ 点的轨迹是什么？并求出其方程；

(Ⅱ)若斜率为 $k$ 的直线 $l$ 与圆 $x^{2} + y^{2} = 1$ 相切，与(Ⅰ)中所求点 $Q$ 的轨迹交于不同的两点 $F, H$ ，且 $\frac{3}{4} \leq \overset{⇀}{O F} \cdot \overset{⇀}{O H} \leq \frac{4}{5}$ （其中 $O$ 是坐标原点）求 $k$ 的取值范围.

查看试题解析