2017年重庆市江北区中考数学一模试卷

试卷更新日期：2017-07-26 类型：中考模拟

进入出卷网下载

一、选择题

1. 3的相反数是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 在下列四个图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 计算6x⁶÷3x²的结果是（）

A、2x³ B、3x⁴ C、2x⁴ D、3x³

查看试题解析
4. 下列调查中，最适宜采用抽样调查方式的是（）

A、对全班同学体能测试达标情况的调查 B、对嘉陵江水域水流污染情况的调查 C、对乘坐飞机的旅客是否携带了违禁物品的检查 D、对奥运会参赛者是否服用了兴奋剂的检查

查看试题解析
5. 如图，直线a直线b被直线c所截，且a∥b，若∠1=40°，则∠2的度数是（）

A、30° B、60° C、120° D、140°

查看试题解析
6. 若△ABC∽△A′B′C′，且△ABC与△A′B′C′的相似比为1：2，则△ABC与△A′B′C′的面积比是（）

A、1：1 B、1：2 C、1：3 D、1：4

查看试题解析
7. 分式 $\frac{1}{x - 2}$ 有意义，则x的取值范围是（）

A、x≠2 B、x≠﹣2 C、x=2 D、x=﹣2

查看试题解析
8. 已知a²+2a﹣3=0，则代数式2a²+4a﹣3的值是（）

A、﹣3 B、0 C、3 D、6

查看试题解析
9. 如图，正方形ABCD的边长为2，连接BD，先以D为圆心，DA为半径作弧AC，再以D为圆心，DB为半径作弧BE，且D、C、E三点共线，则图中两个阴影部分的面积之和是（）

A、 $\frac{1}{2}$ π B、 $\frac{1}{2} π$ +1 C、π D、π+1

查看试题解析
10.
下列图形是由同样大小的棋子按照一定规律排列而成的，其中，图1中有5个棋子，图2中有10个棋子，图3中有16个棋子，…，则图7中有（）个棋子．

A、35 B、40 C、45 D、50

查看试题解析
11.
如图是某水库大坝的横截面示意图，已知AD∥BC，且AD、BC之间的距离为15米，背水坡CD的坡度i=1：0.6，为提高大坝的防洪能力，需对大坝进行加固，加固后大坝顶端AE比原来的顶端AD加宽了2米，背水坡EF的坡度i=3：4，则大坝底端增加的长度CF是（）米．

A、7 B、11 C、13 D、20

查看试题解析
12. 在﹣3、﹣2、﹣1、0、1、2这六个数中，随机取出一个数，记为m，若数m使关于x的分式方程 $\frac{1}{2 x - 1}$ ﹣1= $\frac{m}{1 - 2 x}$ 的解是正实数或零，且使得的二次函数y=﹣x²+（2m﹣1）x+1的图象，在x＞1时，y随x的增大而减小，则满足条件的所有m之和是（）

A、﹣2 B、﹣1 C、0 D、2

查看试题解析

二、填空题

13. 据报道，西部地区最大的客运枢纽系统﹣﹣重庆西站，一期工程已经完成90%，预计在年内建成投入使用．届时，预计每年客流量可达42000000人次，将数42000000用科学记数法表示为．

查看试题解析
14. 计算：（π﹣3）⁰﹣|﹣2|+（﹣ $\frac{1}{2}$ ）^﹣²= ．

查看试题解析
15. 如图，AB是⊙O的直径，点C和点D是⊙O上两点，连接AC、CD、BD，若CA=CD，∠ACD=80°，则∠CAB=°．

查看试题解析
16. 从﹣1，﹣2， $\frac{1}{2}$ ， $\frac{2}{3}$ 四个数中，任取一个数记为k，再从余下的三个数中，任取一个数记为b．则一次函数y=kx+b的图象不经过第四象限的概率是．

查看试题解析
17. 甲、乙两人在1800米长的直线道路上跑步，甲、乙两人同起点、同方向出发，并分别以不同的速度匀速前进．已知，甲出发30秒后，乙出发，乙到终点后立即返回，并以原来的速度前进，最后与甲相遇，此时跑步结束．如图，y（米）表示甲、乙两人之间的距离，t（秒）表示甲出发的时间，图中折线及数据表示整个跑步过程中y与t函数关系．那么，乙到终点后秒与甲相遇．

查看试题解析
18. 如图，正方形ABCD中，F为BC边上的中点，连接AF交对角线BD于G，在BD上截BE=BA，连接AE，将△ADE沿AD翻折得△ADE′，连接E′C交BD于H，若BG=2，则四边形AGHE′的面积是．

查看试题解析

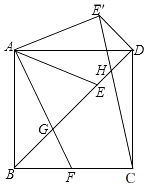
三、解答题

19. 如图，在△ABC和△AEF中，AC∥EF，AB=FE，AC=AF，求证：∠B=∠E．

查看试题解析
20.
为了了解某校初三学生体能水平，体育老师从刚结束的“女生800米，男生1000米”体能测试成绩中随机抽取了一部分同学的成绩，按照“优秀、良好、合格、不合格”进行了统计，并绘制了下列不完整的统计图，
请根据图中信息解答下列问题：

(1)、体育老师总共选取了多少人的成绩？扇形统计图中“优秀”部分的圆心角度数是多少？

(2)、把条形统计图补充完整；

(3)、已知某校初三在校生有2500人，从统计情况分析，请你估算此次体能测试中达到“优秀”水平的大约有多少人？

查看试题解析

四、解答题

21. 计算：

(1)、（2a﹣b）²﹣2b（b﹣2a）

(2)、（x﹣ $\frac{x}{x - 1}$ ）÷ $\frac{x^{3} - 2 x^{2}}{x^{2} - 2 x + 1}$ ﹣ $\frac{x}{x + 1}$ ．

查看试题解析
22. 如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函双y= $\frac{m}{x}$ （m≠0）的阳象交于点c（n，3），与x轴、y轴分别交于点A、B，过点C作CM⊥x轴，垂足为M，若tan∠CAM= $\frac{3}{4}$ ，OA=2．

(1)、求反比例函数和一次函数的解析式；

(2)、点D是反比例函数图象在第三象限部分上的一点，且到x轴的距离是3，连接AD、BD，求△ABD的面积．

查看试题解析
23. 我市“尚品”房地产开发公司预计今年10月份将竣工一商品房小区，其中包括高层住宅区和别墅区一共60万平方米，且高层住宅区的面积不少于别墅区面积的3倍．

(1)、别墅区最多多少万平方米？

(2)、今年一月初，“尚品”公司开始出售该小区，其中高层住宅区的销售单价为8000元/平方米，别墅区的销售单价为12000元/平方米，并售出高层住宅区6万平方米，别墅区4万平方米，二月时，受最新政策“去库存，满足刚需”以及银行房贷利率打折的影响，该小区高层住宅区的销售单价比一月增加了a%，销售面积比一月增加了2a%；别墅区的销售单价比一月份减少了10%，销售面积比一月增加了a%，于是二月份该小区高层住宅区的销售总额比别墅区的销售总额多10080万元，求a的值．

查看试题解析
24. 如图，△ABC和△BDE都是等腰直角三角形，其中∠ACB=∠BDE=90°，AC=BC，BD=ED，连接AE，点F是AE的中点，连接DF．

(1)、如图1，若B、C、D共线，且AC=CD=2，求BF的长度；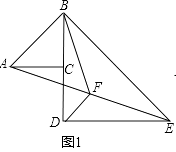

(2)、如图2，若A、C、F、E共线，连接CD，求证：DC= $\sqrt{2}$ DF．

查看试题解析
25. 一个四位数，记千位上和百位上的数字之和为x，十位上和个位上的数字之和为y，如果x=y，那么称这个四位数为“和平数”．
例如：1423，x=1+4，y=2+3，因为x=y，所以1423是“和平数”．

(1)、直接写出：最小的“和平数”是，最大的“和平数”是；

(2)、求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”；

(3)、将一个“和平数”的个位上与十位上的数字交换位置，同时，将百位上与千位上的数字交换位置，称交换前后的这两个“和平数”为一组“相关和平数”．
例如：1423与4132为一组“相关和平数”
求证：任意的一组“相关和平数”之和是1111的倍数．

查看试题解析
26.
如图1，抛物线y=﹣ $\frac{6}{5}$ x²+ $\frac{4 \sqrt{5}}{5}$ x+2的图象与x轴交于点A、B，与y轴交于点C，连接BC，过点A作AD∥BC交抛物线的对称轴于点D．

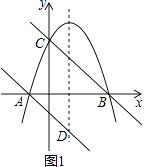
(1)、求点D的坐标；

(2)、
如图2，点P是抛物线在第一象限内的一点，作PQ⊥BC于Q，当PQ的长度最大时，在线段BC上找一点M（不与点B、点C重合），使PM+ $\frac{2}{3}$ BM的值最小，求点M的坐标及PM+ $\frac{2}{3}$ BM的最小值；

(3)、抛物线的顶点为点E，平移抛物线，使抛物线的顶点E在直线AE上移动，点A，E平移后的对应点分别为点A′、E′．在平面内有一动点F，当以点A′、E′、B、F为顶点的四边形为菱形时，求出点A′的坐标．

查看试题解析