2017年四川省资阳市雁江区中考数学模拟试卷（5月份）

试卷更新日期：2017-07-26 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\sqrt{5}$ 的绝对值是（）

A、﹣ $\frac{1}{\sqrt{5}}$ B、﹣ $\sqrt{5}$ C、 $\sqrt{5}$ D、5

查看试题解析
2. 计算a•a⁵﹣（2a³）²的结果为（）

A、a⁶﹣2a⁵ B、﹣a⁶ C、a⁶﹣4a⁵ D、﹣3a⁶

查看试题解析
3. 如图所示，该几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 我国平均每平方千米的土地一年从太阳得到的能量，相当于燃烧130 000 000kg的煤所产生的能量．把130 000 000kg用科学记数法可表示为（）

A、13×10⁷kg B、0.13×10⁸kg C、1.3×10⁷kg D、1.3×10⁸kg

查看试题解析
5. ﹣ $\sqrt{17}$ +1的小数部分是（）

A、﹣ $\sqrt{17}$ +5 B、﹣ $\sqrt{17}$ +4 C、﹣ $\sqrt{17}$ ﹣3 D、 $\sqrt{17}$ ﹣4

查看试题解析
6. 小明记录了一星期天的最高气温如下表，则这个星期每天的最高气温的中位数是（　　）
星期
一
二
三
四
五
六
日
最高气温（℃）
22
24
23
25
24
22
21

A、22℃ B、23℃ C、24℃ D、25℃

查看试题解析
7. 如图，在△ABC中，CA=CB，∠ACB=90°，AB=2，点D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰在弧EF上，则图中阴影部分的面积为（）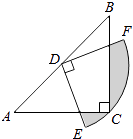

A、 $\frac{π}{2} + \frac{1}{2}$ B、 $π - \frac{1}{4}$ C、 $\frac{π}{4} + \frac{1}{2}$ D、 $\frac{π}{4} - \frac{1}{2}$

查看试题解析
8. 如图，矩形ABCD的顶点A在第一象限，AB∥x轴，AD∥y轴，且对角线的交点与原点O重合．在边AB从小于AD到大于AD的变化过程中，若矩形ABCD的周长始终保持不变，则经过动点A的反比例函数y= $\frac{k}{x}$ （k≠0）中k的值的变化情况是（）

A、一直增大 B、一直减小 C、先增大后减小 D、先减小后增大

查看试题解析
9. 如图，在一张矩形纸片ABCD中，AD=4cm，点E，F分别是CD和AB的中点，现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH，若HG延长线恰好经过点D，则CD的长为（）

A、2cm B、2 $\sqrt{3}$ cm C、4cm D、4 $\sqrt{3}$ cm

查看试题解析
10. 当﹣2≤x≤1时，二次函数y=﹣（x﹣m）²+m²+1有最大值4，则实数m的值为（）

A、﹣ $\frac{7}{4}$ B、 $\sqrt{3}$ 或 $- \sqrt{3}$ C、2或 $- \sqrt{3}$ D、2或 $\sqrt{3}$ 或 $- \frac{7}{4}$

查看试题解析

二、填空题

11. 函数y= $\frac{\sqrt{2 - x}}{x}$ 的自变量取值范围是．

查看试题解析
12. 如图，有以下3个条件：①AC=AB，②AB∥CD，③∠1=∠2，从这3个条件中任选2个作为题设，另1个作为结论，则组成的命题是真命题的概率是．

查看试题解析
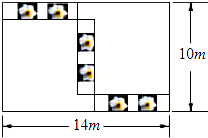
13. 水仙花是漳州市花，如图，在长为14m，宽为10m的长方形展厅，划出三个形状、大小完全一样的小长方形摆放水仙花，则每个小长方形的周长为
m．

查看试题解析
14. 把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为．

查看试题解析
15. 如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为．

查看试题解析
16.
如图，在平面直角坐标系中，A、B两点分别在x轴和y轴上，OA=1，OB= $\sqrt{3}$ ，连接AB，过AB中点C₁分别作x轴和y轴的垂线，垂足分别是点A₁、B₁ ，连接A₁B₁ ，再过A₁B₁中点C₂作x轴和y轴的垂线，照此规律依次作下去，则点C_n的坐标为．

查看试题解析

三、解答题．

17. 先化简，再求值：（x+ $\frac{1 - 2 x}{x}$ ）÷ $\frac{2 x - 2}{x}$ ，其中x= $\sqrt{2}$ +1．

查看试题解析
18. “小组合作学习”成为我区推动课堂教学改革，打造自主高效课堂的重要举措．某中学从全校学生中随机抽取100人作为样本，对“小组合作学习”实施前后学生的学习兴趣变化情况进行调查分析，统计如下：
请结合图中信息解答下列问题：

(1)、小组合作学习前学生学习兴趣为“高”的所占的百分比为；

(2)、补全小组合作学习后学生学习兴趣的统计图；

(3)、通过“小组合作学习”前后学生学习兴趣的对比，请你估计全校2000名学生中学习兴趣获得提高的学生有多少人？

查看试题解析
19. 某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球（每个气排球的价格都相同，每个篮球的价格都相同）．经洽谈，购买1个气排球和2个篮球共需210元；购买2个气排球和3个篮球共需340元．

(1)、每个气排球和每个篮球的价格各是多少元？

(2)、该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个，总费用不超过3200元，且购买气排球的个数少于30个，应选择哪种购买方案可使总费用最低？最低费用是多少元？

查看试题解析
20.
如图，某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图，他们在坡度是i=1：2.5的斜坡DE的D处，测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°，斜坡高EF=2米，CE=13米，CH=2米．大家根据所学知识很快计算出了铁塔高AM．亲爱的同学们，相信你也能计算出铁塔AM的高度！请你写出解答过程．（数据 $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73供选用，结果保留整数）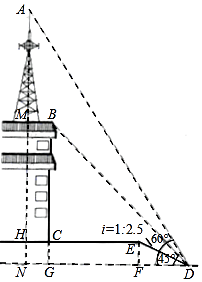

查看试题解析
21. 如图，已知直线y=ax+b与双曲线y= $\frac{k}{x}$ （x＞0）交于A（x₁ ， y₁），B（x₂ ， y₂）两点（A与B不重合），直线AB与x轴交于P（x₀ ， 0），与y轴交于点C．

(1)、若A，B两点坐标分别为（1，3），（3，y₂），求点P的坐标．

(2)、若b=y₁+1，点P的坐标为（6，0），且AB=BP，求A，B两点的坐标．

(3)、结合（1），（2）中的结果，猜想并用等式表示x₁ ， x₂ ， x₀之间的关系（不要求证明）．

查看试题解析
22. 如图，AB是⊙O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC，PB：PC=1：2．

(1)、求证：AC平分∠BAD；

(2)、探究线段PB，AB之间的数量关系，并说明理由；

(3)、若AD=3，求△ABC的面积．

查看试题解析
23.
如图1，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点（不与M、C重合），以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．

(1)、求证：OF∥BE；

(2)、设BP=x，AF=y，求y关于x的函数解析式，并写出自变量x的取值范围；

(3)、
延长DC、FP交于点G，连接OE并延长交直线DC于H（图2），问是否存在点P，使△EFO∽△EHG（E、F、O与E、H、G为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由．

查看试题解析
24.
如图，在平面直角坐标系中，抛物线y=ax²+bx+c与⊙M相交于A、B、C、D四点，其中A、B两点的坐标分别为（﹣1，0），（0，﹣2），点D在x轴上且AD为⊙M的直径．点E是⊙M与y轴的另一个交点，过劣弧 $\hat{E D}$ 上的点F作FH⊥AD于点H，且FH=1.5

(1)、求点D的坐标及该抛物线的表达式；

(2)、若点P是x轴上的一个动点，试求出△PEF的周长最小时点P的坐标；

(3)、在抛物线的对称轴上是否存在点Q，使△QCM是等腰三角形？如果存在，请直接写出点Q的坐标；如果不存在，请说明理由．

查看试题解析

星期	一	二	三	四	五	六	日
最高气温（℃）	22	24	23	25	24	22	21