北师大版数学八年级下册6.2平行四边形的判定同步练习
试卷更新日期：2016-03-03 类型：同步测试
一、选择题
-
1. 能判定四边形ABCD为平行四边形的题设是（ ）A、AB∥CD，AD=BC B、∠A=∠B，∠C=∠D C、AB=CD，AD=BC D、AB=AD，CB=CD2. 下列判断正确的是（ ）A、一组对边平行，另一组对边相等的四边形一定是平行四边形 B、两条对角线互相平分的四边形一定是平行四边形 C、两组邻角分别互补的四边形一定是平行四边形 D、两条对角线相等的四边形一定是平行四边形3. 如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是（ ）
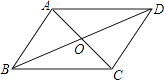A、AB∥CD，AD∥BC B、OA=OC，OB=OD C、AD=BC，AB∥CD D、AB=CD，AD=BC4. 已知四边形ABCD，有以下四个条件：①AB∥CD；②AB=CD；③BC∥AD；④BC=AD．从这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法种数共有（ ）A、6种 B、5种 C、4种 D、3种5. 下列给出的是四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能说明四边形ABCD为平行四边形的是（ ）A、1：2：3：4 B、2：2：3：4 C、2：3：2：3 D、2：3：3：26. 点A ， B ， C是平面内不在同一条直线上的三点，点D是平面内任意一点，若A ， B ， C ， D四点恰能构成一个平行四边形，则在平面内符合这样条件的点D有（ ）A、1个 B、2个 C、3个 D、4个7. 下列选项中的四边形只有一个为平行四边形，根据图中所给的边长长度及角度，判断哪一个为平行四边形？（ ）A、
B、
C、
D、
8. 若以A（-0.5，0）、B（2，0）、C（0，1）三点为顶点要画平行四边形，则第四个顶点不可能在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限9.如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为（ ）
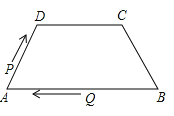A、4s B、3s C、2s D、1s10. 下面几组条件中，能判断一个四边形是平行四边形的是（ ）A、一组对边相等 B、两条对角线互相平分 C、一组对边平行 D、两条对角线互相垂直11. 在下列条件中，不能确定四边形ABCD为平行四边形的是（ ）A、∠A=∠C，∠B=∠D B、∠A=∠B=∠C=90° C、∠A+∠B=180°，∠B+∠C=180° D、∠A+∠B=180°，∠C+∠D=180°12. 根据下列条件，能作出平行四边形的是（ ）A、两组对边的长分别是3和5 B、相邻两边的长分别是3和5，且一条对角线长为9 C、一边的长为7，两条对角线的长分别为6和8 D、一边的长为7，两条对角线的长分别为6和513.如图：在4×4的正方形（每个小正方形的边长均为1）网格中，以A为顶点，其他三个顶点都在格点（网格的交点）上，且面积为2的平行四边形的共有（ ）个．
A、10 B、12 C、14 D、2314.如图，已知△ABC，分别以A，C为圆心，BC，AB长为半径画弧，两弧在直线BC上方交于点D，连接AD，CD，则有（ ）
A、∠ADC与∠BAD相等 B、∠ADC与∠BAD互补 C、∠ADC与∠ABC互补 D、∠ADC与∠ABC互余15.如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（ ）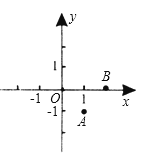
A、（3，-1） B、（-1，-1） C、（1，1） D、（-2，-1）二、填空题
-
16.
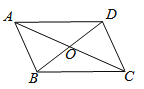
如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件（只添一个即可），使四边形ABCD是平行四边形
17.如图，在梯形ABCD中，CD∥AB，且CD=6cm，AB=9cm，P、Q分别从A、C同时出发，P以1cm/s的速度由A向B运动，Q以2cm/s的速度由C向D运动．则秒时，直线QP将四边形ABCD截出一个平行四边形
18. 用边长为4cm，5cm，6cm的两个全等三角形一共能拼成个平行四边形．19.如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于F点，CD∥AF，请你添加一个条件：使四边形ABCD是平行四边形。
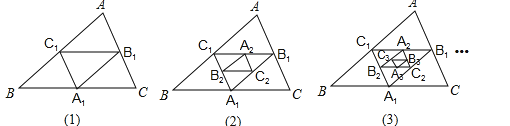
20.如图，在图（1）中，A1、B1、C1分别是△ABC的边BC、CA、AB的中点，在图（2）中，A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点，…，按此规律，则第n个图形中平行四边形的个数共有个
三、解答题
-
21.
嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．
已知：如图1，在四边形ABCD中，BC=AD，
求证：四边形ABCD是 四边形．
（1）在方框中填空，以补全已知和求证；
（2）按嘉淇的想法写出证明；
（3）用文字叙述所证命题的逆命题为平行四边形两组对边分别相等
22.如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．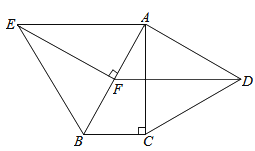
(1)、试说明AC=EF；(2)、求证：四边形ADFE是平行四边形.
23.已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．
(1)、求证：△BCG≌△DCE；(2)、将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。24. 我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．请解答下列问题：(1)、写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；(2)、探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论．25.如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF．
(1)、请在图中找出一对全等三角形，用符号“≌”表示，并加以证明；(2)、判断四边形ABDF是怎样的四边形，并说明理由；(3)、若AB=6，BD=2DC，求四边形ABEF的面积．