浙江省台州市椒江区2016-2017学年七年级下学期数学期末考试
试卷更新日期:2017-07-26 类型:期末考试
一、选择题
-
1. 的相反数是( )A、 B、 C、 D、22. 平面直角坐标系中的点P(2,-1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3.
如图,直线l1//l2 , 直线l3与l1 , l2分别交于A,B两点,若∠1=65°,则∠2=( )
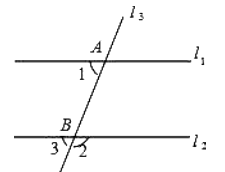 A、65° B、115° C、125° D、135°4. 下列调查适合抽样调查的是( )A、改一位学生作文中的错别字 B、对班级的卫生死角进行调查 C、对八名同学的身高情况进行调查 D、对电视剧《人民的名义》收视率进行调查5. 下列命题中,是假命题的是( )A、相等的角是对顶角 B、垂线段最短 C、两直线平行,同旁内角互补 D、两点确定一条直线6. 实数-2,0.101001…(相邻的两个1之间依次增加一个0), , ,-π中,无理数的个数是( )A、2个 B、3个 C、4个 D、5个7. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、
A、65° B、115° C、125° D、135°4. 下列调查适合抽样调查的是( )A、改一位学生作文中的错别字 B、对班级的卫生死角进行调查 C、对八名同学的身高情况进行调查 D、对电视剧《人民的名义》收视率进行调查5. 下列命题中,是假命题的是( )A、相等的角是对顶角 B、垂线段最短 C、两直线平行,同旁内角互补 D、两点确定一条直线6. 实数-2,0.101001…(相邻的两个1之间依次增加一个0), , ,-π中,无理数的个数是( )A、2个 B、3个 C、4个 D、5个7. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、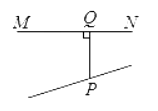 B、
B、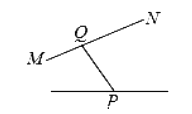 C、
C、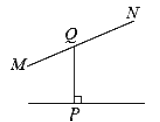 D、
D、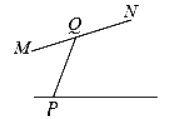 8.
8.如图,在隐去原点的数轴上标注了四段范围,则表示 的点落在( )
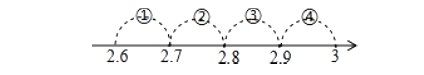 A、段① B、段② C、段③ D、段④9.
A、段① B、段② C、段③ D、段④9.如图,直线l1//l2 , ∠α=∠β,∠1=45°,则∠2的度数为( )
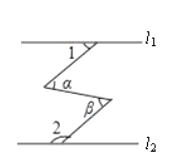 A、145° B、135° C、125° D、115°10. 如果若干个一元一次方程的根都是整数且是一元一次不等式组所有整数解,则称这些一元一次方程为该不等式组的紧密关联方程.如不等式组 ,可以有紧密关联方程x-1=0 , x-2=0,x-3=0;(不固定),若方程3-x=2x,2x=4都是关于x的不等式组 的紧密关联方程,则m的取值范围为( )A、-1<m≤0 B、1≤m<2 C、0≤m<1 D、2<m≤3
A、145° B、135° C、125° D、115°10. 如果若干个一元一次方程的根都是整数且是一元一次不等式组所有整数解,则称这些一元一次方程为该不等式组的紧密关联方程.如不等式组 ,可以有紧密关联方程x-1=0 , x-2=0,x-3=0;(不固定),若方程3-x=2x,2x=4都是关于x的不等式组 的紧密关联方程,则m的取值范围为( )A、-1<m≤0 B、1≤m<2 C、0≤m<1 D、2<m≤3二、填空题
-
11. 已知 是方程mx+y=1的解,则m=.12. 已知点P(a-2,a)在x轴上,那么a=.13. 已知一个样本的容量为50,在频数分布直方图中,各小长方形高之比为2:4:1:3,第二组的频数是.14. 计算 =(结果保留根号)15. 平面直角坐标系中的点P(-2,3),将点P向左平移2个单位长度,再向下平移1个单位长度,得到点P‘的坐标是.16. 已知整数k满足k< <k+1,则k的值为.17.
如图,长方形纸片ABCD沿EF折叠后,ED交BC于点G,点D,C分别落在点D’、C’位置上,若∠EFG=55°,∠BGE=度.
 18.
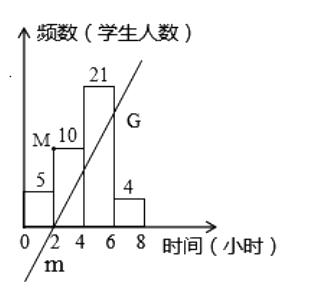
18.为了了解我区某校“校园阅读”的建设情况,检查组随机抽取40名学生,调查他们一周阅读课外书籍的时间,并将结果绘成了频数分布直方图,我们把每一个直方图的时间与学生数的积看成直方图的“面积”,时间为横轴,学生人数为纵轴构成直角坐标系,规定点M的坐标为(2,10),直线m经过点(2,0)交直方图于一点G,直线m把四个直方图面积分成相等两部分,则G点坐标为.
三、解答题
-
19. 综合题。(1)、计算:(2)、解方程组:20. 解不等式组: ,并在数轴上表示出不等式组的解集.21.
在△ABC中,F是BC上一点,FG⊥AB,垂足为G.
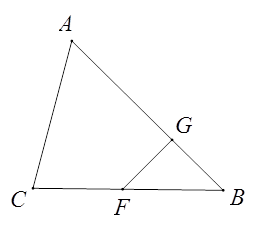 (1)、过C点画CD⊥AB,垂足为D;(2)、过D点画DE//BC,交AC于E;(3)、说明∠EDC=∠GFB的理由.22.
(1)、过C点画CD⊥AB,垂足为D;(2)、过D点画DE//BC,交AC于E;(3)、说明∠EDC=∠GFB的理由.22.某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.
组别
听写正确的个数x
人数
A
0≤x<8
10
B
8≤x<16
15
C
16≤x<24
25
D
24≤x<32
m
E
32≤x<40
n
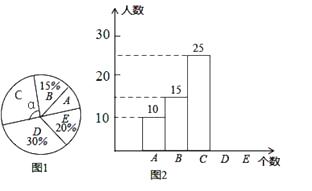
根据以上信息解决下列问题:
(1)、本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;(2)、求出图1中∠α的度数;(3)、该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数23. 星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如下表:进价(元/台)
售价(元/台)
电饭煲
200
250
电压锅
160
200
(1)、一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?(2)、为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ,橱具店有哪几种进货方案?并说明理由.(3)、在(2)的条件下,直接写出橱具店赚钱最多的进货方案.24.在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足 .
 (1)、a为不等式2x+6<0的最大整数解,求a的值并判断点A在第几象限;(2)、在(1)的条件下,求△AOB的面积;(3)、在(2)的条件下,若两个动点M(k-1,k),N(-2h+10,h),请你探索是否存在以两个动点M、N为端点的线段MN//AB,且MN=AB,若存在,求M、N两点的坐标;若不存在,请说明理由.
(1)、a为不等式2x+6<0的最大整数解,求a的值并判断点A在第几象限;(2)、在(1)的条件下,求△AOB的面积;(3)、在(2)的条件下,若两个动点M(k-1,k),N(-2h+10,h),请你探索是否存在以两个动点M、N为端点的线段MN//AB,且MN=AB,若存在,求M、N两点的坐标;若不存在,请说明理由.