浙江省宁波市北仑区2018-2019学年七年级上学期期末考试数学试题
试卷更新日期:2019-12-13 类型:期末考试
一、单选题
-
1. 2019的相反数是( )A、 B、-2019 C、 D、20192. 据报道,某万人沙滩规划面积约32万平方米.数字32万用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 在 ,0.2, , ,1.010010001…(每两个1之间依次增加一个0)中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个5. 已知 和 是同类项,则 的值为( )A、3 B、4 C、5 D、66. 关于 的方程 与 的解相同,则 的值为( )A、3 B、4 C、5 D、67. 《九章算术》中记载一问题如下:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”意思是:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱,问人数、物价各多少?设有 人,依题意列方程得( )A、 B、 C、 D、8. 如图, 方向是北偏西 方向, 平分 ,则 的度数为( )
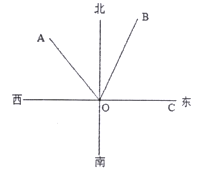 A、 B、 C、 D、9. 利用如图1的二维码可以进行身份识别,某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20。如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生,表示6班学生的识别图案是( )
A、 B、 C、 D、9. 利用如图1的二维码可以进行身份识别,某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20。如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生,表示6班学生的识别图案是( )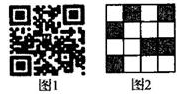 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
10. 如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( ) A、29 B、28 C、30 D、31
A、29 B、28 C、30 D、31二、填空题
-
11. 如果向东走2米记为+2米,则向西走3米可记为米.12. 单项式 的系数为 .13. 36的平方根是 , 的立方根是 , - 的绝对值是 .14. 若 ,则 .15. 如图,线段 , 是 上一点,且 , 是 中点,则线段 的长度为 .
 16. 如图,在长方形 中, 比 大 ,则 的度数为(用度分秒形式表示).
16. 如图,在长方形 中, 比 大 ,则 的度数为(用度分秒形式表示). 17. 数轴上从左到右依次有 三点, 三点表示的数分别为 , , ,其中 为整数,且满足 ,则 .18. “格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出,在明代的《算法统宗》一书中被称为“铺地锦”.如图1,计算 ,将乘数47记入上行,乘数51记入右行.然后以乘数47的每位数字乘以乘数51的每位数字,将结果记入相应的格子中,最后按斜行加起来,既得2397.图2用“格子乘法”表示两个两位数相乘,则 的值为.
17. 数轴上从左到右依次有 三点, 三点表示的数分别为 , , ,其中 为整数,且满足 ,则 .18. “格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出,在明代的《算法统宗》一书中被称为“铺地锦”.如图1,计算 ,将乘数47记入上行,乘数51记入右行.然后以乘数47的每位数字乘以乘数51的每位数字,将结果记入相应的格子中,最后按斜行加起来,既得2397.图2用“格子乘法”表示两个两位数相乘,则 的值为.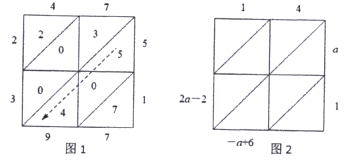
三、解答题