浙江省绍兴市嵊州市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-12-13 类型：期末考试
一、单选题
-
1. 如图，一扇窗户打开后，用窗钩 AB 可将其固定，这里所运用的几何原理是（ ）
A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、三角形的稳定性2. 不等式x+1≥2的解集在数轴上表示正确的是（ ）A、
B、
C、
D、
3. 长度分别为2，6，x的三条线段能组成一个三角形，x的值可以是（ ）A、2 B、4 C、6 D、84. 如果一元二次方程2x2+3x+m=0有两个相等的实数根，那么实数m的取值为（ ）A、m＞ B、m C、m= D、m=5. 关于 的叙述正确的是（ ）A、在数轴上不存在表示 的点 B、 ＝ + C、 ＝±2 D、与 最接近的整数是36. 如图，在平面直角坐标系中，一次函数 经过 ， 两点，则不等式 的解是（ ）
A、 B、 C、 D、7. 如图，在△ABC中，以点B为圆心，以BA长为半径画弧交边BC于点D，连接AD，若∠B=30°，∠C=40°，则∠DAC的度数是（ ）
A、25° B、35° C、45° D、75°8. 一个有进水管和出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（L）与时间x（min）之间的关系如图所示，则每分钟的进水量与出水量分别是（ ）
A、5L，3.75L B、2.5L，5L C、5L，2.5L D、3.75L，5L9. 下面所说的“平移”，是指只沿方格的格线（即左右或上下）运动，并将图中的任一条线段平移一格称为“1步”．通过平移，使得图中的3条线段首尾相接组成一个三角形，最少需要移动的步数是（ ）
A、7步 B、8步 C、9步 D、10步10. 如图，在平面直角坐标系xOy中，A（4，0），B（0，3），点D在x轴上，若在线段AB（包括两个端点）上找点P，使得点A，D，P构成等腰三角形的点P恰好只有1个．下列选项中满足上述条件的点D坐标不可以是（ ）
A、（﹣3，0） B、（1，0） C、（5，0） D、（9，0）二、填空题
-
11. 命题：“若a=b ， 则a2=b2”，写出它的逆命题： ．12. 已知不等式﹣4x≤﹣8，两边同时除以“﹣4”得13. 若将方程x2+2x﹣1=0配方成（x+a）2=h的形式，则a+h的值是 ．14. 等腰三角形的一边长为3，另一边长为6，则该三角形的周长是 ．15. 如图，小巷左右两侧是竖直的墙，已知小巷的宽度是2.2米，一架梯子斜靠在左墙时，梯子底端到坐墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端距离地面米.
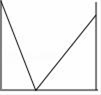16. 如图，已知△ABC≌△EDF，点F，A，D在同一条直线上，AD是∠BAC的平分线，∠EDA=30°，∠E=70°，则∠ADC的度数是 ．
17. 如图，在平面直角坐标系中，△OAB是等腰直角三角形，∠OAB=90°，已知点A（4，3），点B在第四象限，则点B的坐标是 ．
18. 定义：在平面直角坐标系中，把从点P出发沿横或纵方向到达点Q（至多拐一次弯）的路径长称为P，Q的“实际距离”．如图，若P（﹣1，1），Q（2，3），则P，Q的“实际距离”为5，即PS+SQ=5或PT+TQ=5．环保低碳的公共自行车，逐渐成为市民出行喜欢的交通工具．设A，B，C三个小区的坐标分别为A（3，3），B（6，﹣2），C（0，﹣4），若点M表示公共自行车停放点，且满足M到A，B，C的“实际距离”相等，则点M的坐标是 ．
19. 已知等边三角形ABC中，AB=4，点D是边AB的中点，点E是边BC上的动点，连接DE，将△BDE沿直线DE翻折，点B的对应点为B′，当直线B′E与直线AC的夹角为30°时，BE的长度是 ．
20. 已知，在△ABC中，∠A＞∠B，分别以点A，C为圆心，大于 AC长为半径画弧，两弧交于点P，点Q，作直线PQ交AB于点D，再分别以点B，D为圆心，大于 BD长为半径画弧，两弧交于点M，点N，作直线MN交BC于点E，若△CDE是等边三角形，则∠A= ．
三、解答题
-
21.(1)、解不等式组：(2)、解方程：2x2﹣4x﹣3=0．22. 在如图的正方形网格中，每一个小正方形的边长为1，格点三角形ABC（顶点是网格线交点的三角形）的顶点A，B的坐标分别是（﹣6，7），（﹣4，3）．
(1)、请你根据题意在图中的网格平面内作出平面直角坐标系．(2)、请画出△ABC关于y轴对称的△A1B1C123. “和谐号”火车从车站出发，在行驶过程中速度y（单位：m/s）与时间x（单位：s）的关系如图所示，其中线段BC∥x轴．请根据图象提供的信息解答下列问题：
(1)、当0≤x≤10，求y关于x的函数解析式；(2)、求C点的坐标．24. 如图，在Rt△ACB中，∠ACB=90º，点D是AB的中点，点E是CD的中点，过C作CF∥AB交AE的延长线于点F，连BF.
(1)、求证：△ADE≌△FCE；(2)、若∠DCF=120º，DE=2，求BC的长.25. 已知：如图1，在平面直角坐标系中，一次函数y＝ x+3交x轴于点A，交y轴于点B，点C是点A关于y轴对称的点，过点C作y轴平行的射线CD，交直线AB与点D，点P是射线CD上的一个动点．
(1)、求点A，B的坐标．(2)、如图2，将△ACP沿着AP翻折，当点C的对应点C′落在直线AB上时，求点P的坐标．(3)、若直线OP与直线AD有交点，不妨设交点为Q(不与点D重合)，连接CQ，是否存在点P，使得S△CPQ＝2S△DPQ ， 若存在，请求出对应的点Q坐标；若不存在，请说明理由．