浙江省宁波市奉化区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-12-13 类型：期末考试
一、单选题
-
1. 下面四个汽车标志图标中，不是轴对称图形的为（ ）A、
B、
C、
D、
2. 下列长度的三条线段能组成三角形的是（ ）A、1，2，3 B、3，4，5 C、5，6，11 D、4，5，103. 已知 ，则下列不等式变形正确的是（ ）A、 B、 C、 D、4. 下面给出的四个三角形都有一部分被遮挡，其中不能确定三角形类型的是（ ）A、
B、
C、
D、
5. 对于命题“如果∠1+∠2=90°，那么∠1≠∠2．”能说明它是假命题的是（ ）A、 ， B、 ， C、 ， D、6. 如图，已知∠1=∠2，欲得到△ABD≌△ACD，则从下列条件中补选一个，错误的选法是（ ）
A、 B、 C、 D、7. 一次函数y=kx+b经过第一、三、四象限，则下列正确的是（ ）A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜08. 将一个有45°角的三角板的直角顶点C放在一张宽为5cm的纸带边沿上，另一个顶点B在纸带的另一边沿上，测得∠DBC=30°，则三角板的最大边的长为（ ）
A、5cm B、10cm C、 D、9. 有下列说法：①有一个角为60°的等腰三角形是等边三角形；②三边分别是1， ，3的三角形是直角三角形；③直角三角形斜边上的中线等于斜边的一半；④三个角之比为3：4：5的三角形是直角三角形，其中正确的有（ ）A、1个 B、2个 C、3个 D、4个10. 某次知识竞赛试卷有20道题，评分办法是答对一道记5分，不答记0分，答错一道扣2分，小明有3道题没答，但成绩超过60分，则小明至少答对了（ ）道题．A、13 B、14 C、15 D、1611. 直角三角形纸片的两直角边长分别为6，8，现将△ABC按如图那样折叠，使点A与点B重合，折痕为DE，则DE的长为（ ）
A、 B、5 C、 D、12. 在等腰三角形△ABC（AB=AC，∠BAC=120°）所在平面上有一点P，使得△PAB，△PBC，△PAC都是等腰三角形，则满足此条件的点P有（ ）A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知一个正比例函数的图象经过点（-2，4）， 则这个正比例函数的表达式是14. 若点A（2，n）在x轴上，则点B（n+2，n-5）位于第象限．15. 如图，已知Rt△ABC ， ∠C＝90°，BD是角平分线，BD＝5，BC＝4，则D点到AB的距离是 ．
16. 已知一次函数y=kx+b的图象如图所示，则不等式kx+b≥4的解是 ．
17. 如图，在锐角△ABC中，AB=5 ，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD，AB上的动点，则BM+MN的最小值是 ．
三、解答题
-
18. 解不等式组 ，并把不等式组的解在数轴上表示出来.
19. 如图所示，在△ABC中，AB=AC，∠1=∠2，AD⊥CD于点D，AE⊥BE于点E，BE，CD交于点O．
求证：
(1)、△ABE≌△ACD；
(2)、OD=OE．20. 两个城镇A、B与两条公路l1、l2位置如图所示，电信部门需在C处修建一座信号反射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路l1 ， l2的距离也必须相等，那么点C应选在何处？请在图中，用尺规作图找出所有符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）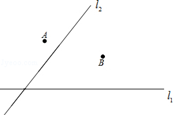
21. 如图，一次函数 的图象分别与 轴、 轴交于点 、 ，以线段 为边在第一象限内作等腰 ， .
(1)、求 点的坐标(2)、求过 、 两点直线的函数表达式．22. 浙江实施“五水共治“以来，越来越重视节约用水，某地对居民用水按阶梯水价方式进行收费，人均月生活用水收费标准如图所示，图中x表示人均月生活用水的吨数，y表示收取的人均月生活用水费（元），请根据图象信息，回答下列问题.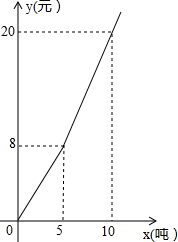
(1)、请写出y与x的函数关系式；(2)、若某个家庭有5人，响应节水号召，计划控制1月份的生活用水费不超过76元，则该家庭这个月最多可以用多少吨水？23. 如图，已知AC∥BD，AE，BE分别平分∠CAB和∠DBA，点E在线段CD上．
(1)、求∠AEB的度数；(2)、求证：CE=DE．24. 定义：若以三条线段a，b，c为边能构成一个直角三角形，则称线段a，b，c是勾股线段组．
(1)、如图①，已知点M，N是线段AB上的点，线段AM，MN，NB是勾股线段组，若AB=12，AM=3，求MN的长；(2)、如图②，△ABC中，∠A=18°，∠B=27°，边AC，BC的垂直平分线分别交AB于点M，N，求证：线段AM，MN，NB是勾股线段组；(3)、如图③，在等边△ABC中，P为△ABC内一点，线段AP，BP，CP构成勾股线段组，CP为此线段组的最长线段，求∠APB的度数．