浙江省金华市婺城区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-12-13 类型:期末考试
一、单选题
-
1. 下列各组数可能是一个三角形的边长的是( )A、1,2,4 B、4,5,9 C、4,6,8 D、5,5,112. 如图,小手盖住的点的坐标可能是( )
 A、(3,3) B、(﹣4,5) C、(﹣4,﹣6) D、(3,﹣6)3. 若a>b , 则下列不等式中正确的是( )A、 B、 C、 D、4. “若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=﹣2 B、a=﹣2,b=3 C、a=2,b=﹣3 D、a=﹣3,b=25. 下列条件中,不能判断一个三角形为直角三角形的是A、三个角的比是1:2:3 B、三条边满足关系 C、三条边的比是2:3:4 D、三个角满足关系6. 将直线 向左平移2个单位所得的直线的解析式是( )A、 B、 C、 D、7. 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )
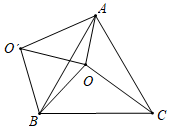
A、(3,3) B、(﹣4,5) C、(﹣4,﹣6) D、(3,﹣6)3. 若a>b , 则下列不等式中正确的是( )A、 B、 C、 D、4. “若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=﹣2 B、a=﹣2,b=3 C、a=2,b=﹣3 D、a=﹣3,b=25. 下列条件中,不能判断一个三角形为直角三角形的是A、三个角的比是1:2:3 B、三条边满足关系 C、三条边的比是2:3:4 D、三个角满足关系6. 将直线 向左平移2个单位所得的直线的解析式是( )A、 B、 C、 D、7. 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )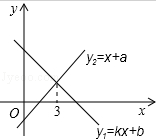 A、1 B、2 C、3 D、48. 如图,O是正 内一点, , , ,将线段BO以点B为旋转中心逆时针旋转 得到线段 ,下列五个结论中,其中正确的结论是( )
A、1 B、2 C、3 D、48. 如图,O是正 内一点, , , ,将线段BO以点B为旋转中心逆时针旋转 得到线段 ,下列五个结论中,其中正确的结论是( )可以由 绕点B逆时针旋转 得到; 点O与 的距离为4; ; ; .
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图是2002年在北京召开的世界数学家大会的会标,其中央图案正是经过艺术处理的“弦图”,它蕴含着一个著名的定理是 .
 10. 如图,∠ABC=∠DCB,请补充一个条件: , 使△ABC≌△DCB.
10. 如图,∠ABC=∠DCB,请补充一个条件: , 使△ABC≌△DCB.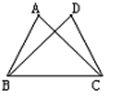 11. 不等式 的正整数解是 .12. 如图,在 中, , 的平分线BD交AC于点D , , , ,则在 中,BD边上的高为 .
11. 不等式 的正整数解是 .12. 如图,在 中, , 的平分线BD交AC于点D , , , ,则在 中,BD边上的高为 .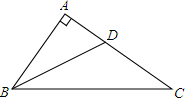
三、解答题
-
13. 某批服装进价为每件200元,商店标价每件300元,现商店准备将这批服装打折出售,但要保证毛利润不低于 ,问售价最低可按标价的几折? 要求通过列不等式进行解答14. 解不等式组15. 如图,AB与CD相交于点E , , 求证: .
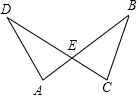 16. 如图,在 中,AE是 的角平分线,AD是BC边上的高,且 , ,求 、 的度数.
16. 如图,在 中,AE是 的角平分线,AD是BC边上的高,且 , ,求 、 的度数. 17. 如图是由边长为1的小正方形组成的网格图.
17. 如图是由边长为1的小正方形组成的网格图.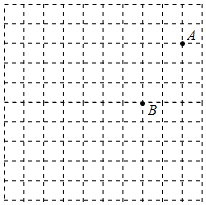 (1)、请在网格图中建立平面直角坐标系xOy , 使点A的坐标为 ,点B的坐标为 ;(2)、若点C的坐标为 , 关于y轴对称三角形为 ,则点C的对应点 坐标为;(3)、已知点D为y轴上的动点,求 周长的最小值.18. 甲、乙两车都从A地驶向B地,并以各自的速度匀速行驶 甲车比乙车早行驶,甲车途中休息了 设甲车行驶时间为 ,下图是甲乙两车行驶的距离 与 的函数图象,根据题中信息回答问题:
(1)、请在网格图中建立平面直角坐标系xOy , 使点A的坐标为 ,点B的坐标为 ;(2)、若点C的坐标为 , 关于y轴对称三角形为 ,则点C的对应点 坐标为;(3)、已知点D为y轴上的动点,求 周长的最小值.18. 甲、乙两车都从A地驶向B地,并以各自的速度匀速行驶 甲车比乙车早行驶,甲车途中休息了 设甲车行驶时间为 ,下图是甲乙两车行驶的距离 与 的函数图象,根据题中信息回答问题: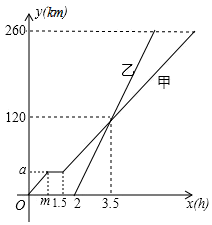 (1)、填空: , ;(2)、当乙车出发后,求乙车行驶路程 与 的函数解析式,并写出相应的x的取值范围;(3)、当甲车行驶多长时间时,两车恰好相距50km?请直接写出答案.19. 定义:如果经过三角形一个顶点的线段把这个三角形分成两个小三角形,其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么这条线段称为原三角形的“和谐分割线”,例如:如图1,等腰直角三角形斜边上的中线就是一条“和谐分割线”
(1)、填空: , ;(2)、当乙车出发后,求乙车行驶路程 与 的函数解析式,并写出相应的x的取值范围;(3)、当甲车行驶多长时间时,两车恰好相距50km?请直接写出答案.19. 定义:如果经过三角形一个顶点的线段把这个三角形分成两个小三角形,其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么这条线段称为原三角形的“和谐分割线”,例如:如图1,等腰直角三角形斜边上的中线就是一条“和谐分割线” (1)、判断下列两个命题是真命题还是假命题 填“真”或“假”
(1)、判断下列两个命题是真命题还是假命题 填“真”或“假”等边三角形必存在“和谐分割线”
如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”.
命题 是命题,命题 是命题;
(2)、如图2, , , , ,试探索 是否存在“和谐分割线”?若存在,求出“和谐分割线”的长度;若不存在,请说明理由.(3)、如图3, 中, ,若线段CD是 的“和谐分割线”,且 是等腰三角形,求出所有符合条件的 的度数.20. 如图,直线 与x轴、y轴分别交于点 、 ,点P在x轴上运动,连接PB , 将 沿直线BP折叠,点O的对应点记为 .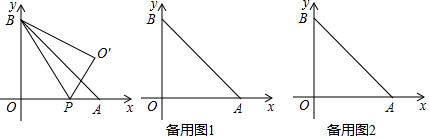 (1)、求k、b的值;(2)、若点 恰好落在直线AB上,求 的面积;(3)、将线段PB绕点P顺时针旋转 得到线段PC , 直线PC与直线AB的交点为Q , 在点P的运动过程中,是否存在某一位置,使得 为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求k、b的值;(2)、若点 恰好落在直线AB上,求 的面积;(3)、将线段PB绕点P顺时针旋转 得到线段PC , 直线PC与直线AB的交点为Q , 在点P的运动过程中,是否存在某一位置,使得 为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.