浙江省杭州市下城区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-13 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点P（3，﹣2）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 以下列各组线段为边，能组成三角形的是（）

A、2cm ， 5 cm ， 8cm B、3 cm ， 3 cm ， 6 cm C、3 cm ， 4 cm ， 5 cm D、1 cm ， 2cm ， 3 cm

查看试题解析
3. 下列命题中，真命题是（）

A、若 2x＝﹣1，则 x＝﹣2 B、任何一个角都比它的补角小 C、等角的余角相等 D、一个锐角与一个钝角的和等于一个平角

查看试题解析
4. 下列说法正确的是（）

A、x＝﹣3是不等式x＞﹣2的一个解 B、x＝﹣1是不等式x＞﹣2的一个解 C、不等式x＞﹣2的解是x＝﹣3 D、不等式x＞﹣2的解是x＝﹣1

查看试题解析
5. 若等腰三角形的一边长是4，则它的周长可能是（）

A、7 B、8 C、9 D、8或9

查看试题解析
6. 已知3a＞﹣6b ，则下列不等式一定成立的是（）

A、a+1＞﹣2b﹣1 B、﹣a＜b C、3a+6b＜0 D、 $\frac{a}{b}$ ＞﹣2

查看试题解析
7. 已知点A的坐标为（a+1，3﹣a），下列说法正确的是（）

A、若点A在y轴上，则a＝3 B、若点A在一三象限角平分线上，则a＝1 C、若点A到x轴的距离是3，则a＝±6 D、若点A在第四象限，则a的值可以为﹣2

查看试题解析
8. 一次函数y＝kx+b（k≠0）的图象经过点B（﹣6，0），且与正比例函数y＝ $\frac{1}{3}$ x的图象交于点A（m ， ﹣3），若kx﹣ $\frac{1}{3}$ x＞﹣b ，则（）

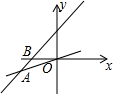A、x＞0 B、x＞﹣3 C、x＞﹣6 D、x＞﹣9

查看试题解析
9. 如图，在△ABC中，∠B＞90°，CD为∠ACB的角平分线，在AC边上取点E，使DE＝DB，且∠AED＞90°.若∠A＝α，∠ACB＝β，则（）

A、∠AED＝180°﹣α﹣β B、∠AED＝180°﹣α﹣ $\frac{1}{2}$ β C、∠AED＝90°﹣α+β D、∠AED＝90°+α+ $\frac{1}{2}$ β

查看试题解析
10. 速度分别为100km/h和akm/h（0＜a＜100）的两车分别从相距s千米的两地同时出发，沿同一方向匀速前行．行驶一段时间后，其中一车按原速度原路返回，直到与另一车相遇时两车停止．在此过程中，两车之间的距离y（km）与行驶时间t（h）之间的函数关系如图所示．下列说法：①a＝60；②b＝2；③c＝b+ $\frac{5}{2}$ ；④若s＝60，则b＝ $\frac{3}{2}$ ．其中说法正确的是（）

A、①②③ B、②③④ C、①②④ D、①③④

查看试题解析

二、填空题

11. 在△ABC中，∠A＝50°，若∠B比∠A的2倍小30°，则△ABC是三角形．

查看试题解析
12. 点A（﹣2，﹣3）向上平移3个单位得到的点的坐标为．

查看试题解析
13. “x的7倍减去1是正数”用不等式表示为．

查看试题解析
14. 如图，在△ABC中，AD垂直平分BC ，交BC于点E ， CD⊥AC ，若AB＝6，CD＝3，则BE＝．

查看试题解析
15. 在平面直角坐标系中，点A坐标为（﹣3，m+2），点B坐标为（1，m﹣2），若点C（t+1，n₁）和点D（t﹣2，n₂）均在直线AB上，则n₁﹣n₂＝．

查看试题解析
16. 如图，已知△ABC和△ADE均为等边三角形，点O是AC的中点，点D在射线BO上，连结OE ， EC ，则∠ACE＝°；若AB＝1，则OE的最小值＝．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 2 x - 4 < 0 \\ \frac{1}{2} (x + 8) - 2 > 0 \end{array}$ 并把解在数轴上表示出来．

查看试题解析
18. 如图，△ABC的顶点均在格点上．

(1)、分别写出点A ，点B ，点C的坐标．

(2)、若△A'B'C'与△ABC关于y轴对称，在图中画出△A'B'C'，并写出相应顶点的坐标．

查看试题解析
19. 如图，在Rt△ABC中，AB＝AC ， P为斜边BC上一点（PB＜CP），分别过点B ， C作BE⊥AP于点E ， CD⊥AP于点D ．

(1)、求证：AD＝BE；

(2)、若AE＝2DE＝2，求△ABC的面积．

查看试题解析
20. 2019年1月同一时刻北京时间与英国伦敦时间分别为20：00和12：00．设北京时间为t（时），伦敦时间为y（时）．

(1)、请在表格的空格内填入合适的数字；

北京时间

8：30

22：30

伦敦时间

12：10

(2)、当8≤t≤24时，请直接写出y关于t的函数表达式；

(3)、如果一航班在1月10日于北京时间13：00从上海起飞，到达英国伦敦当地时间为1月10日17：30，求该航班在途中经历了多少时间？

查看试题解析
21. 如图，在△ABC中，AD是△ABC的高线，CE是△ABC的角平分线，它们相交于点P．

(1)、若∠B＝40°，∠AEC＝75°，求证：AB＝BC；

(2)、若∠BAC＝90°，AP为△AEC边EC上中线，求∠B的度数．

查看试题解析
22. 如图，在△ABC中，AB＝AC ， BD平分∠ABC交AC于点D ，点E是BC延长线上的一点，且BD＝DE ．点G是线段BC的中点，连结AG ，交BD于点F ，过点D作DH⊥BC ，垂足为H ．

(1)、求证：△DCE为等腰三角形；

(2)、若∠CDE＝22.5°，DC＝ $\sqrt{2}$ ，求GH的长；

(3)、探究线段CE ， GH的数量关系并用等式表示，并说明理由．

查看试题解析
23. 已知一次函数 $y_{1} = (a - 1) x - 2 a + 1$ ，其中 $a \neq 1$ .

(1)、若点 $(1, - \frac{1}{2})$ 在y₁的图象上.求a的值:

(2)、当 $- 2 ⩽ x ⩽ 3$ 时.若函数有最大值2.求y₁的函数表达式;

(3)、对于一次函数 $y_{2} = (m + 1) (x - 1) + 2$ ，其中 $m \neq - 1$ ，若对一切实数x， $y_{1} < y_{2}$ 都成立，求a，m需满足的数量关系及 a的取值范围.

查看试题解析

北京时间	8：30		22：30
伦敦时间		12：10