浙江省杭州市临安市2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-12-13 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 a＝3cm，b＝6cm，则下列长度的线段中，能与 a ， b 组成三角形的是（）

A、2cm B、6cm C、9cm D、11cm

查看试题解析
2. 在平面直角坐标系中，点 M(a²＋1，－3)所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 正比例函数 $y = (k - 2) x$ 中，y随x的增大而减小，则k的取值范围是（）

A、 $k \geq 2$ B、 $k \leq 2$ C、 $k > 2$ D、 $k < 2$

查看试题解析
4. 不等式 1－x＞0 的解在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 下列判断正确的是（）

A、两边和一角对应相等的两个三角形全等 B、一边及一锐角相等的两个直角三角形全等 C、顶角和底边分别相等的两个等腰三角形全等 D、三个内角对应相等的两个三角形全等

查看试题解析
6. 已知 a＞b ，则下列四个不等式中，不正确的是（）

A、a －3＞ b －3 B、－ a ＋2＞－ b ＋2 C、 $\frac{1}{5}$ a＞ $\frac{1}{5}$ b D、1+4a＞1+4b

查看试题解析
7. 已知(－1，y₁)，(1.8，y₂)，(- $\frac{1}{2}$ ， y₃)是直线 y = -3x + m (m 为常数)上的三个点，则 y₁ ， y₂ ， y₃的大小关系是（）

A、y₃＞y₁＞y₂ B、y₁＞y₃＞y₂ C、y₁＞y₂＞y₃ D、y₃＞y₂＞y₁

查看试题解析
8. 如图，给出下列四个条件，AB=DE，BC=EF，∠B=∠E，∠C=∠F，从中任选三个条件能使△ABC≌△DEF的共有（）

A、1组 B、2组 C、3组 D、4组

查看试题解析
9. 如图，直线y=3x+6与x，y轴分别交于点A，B，以OB为底边在y轴右侧作等腰△OBC，将点C向左平移5个单位，使其对应点C′恰好落在直线AB上，则点C的坐标为（）

A、（3，3） B、（4，3） C、（﹣1，3） D、（3，4）

查看试题解析
10. 如图，∠AOB＝30°，∠AOB 内有一定点 P，且 OP＝12，在 OA 上有一动点 Q，OB 上有一动点 R。若△PQR 周长最小，则最小周长是（）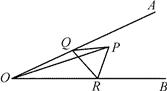

A、6 B、12 C、16 D、20

查看试题解析

二、填空题

11. 命题“如果a²=b² ，那么a=b”的逆命题是命题．（填写“真”或“假”）

查看试题解析
12. 如图，在平面直角坐标系中，点P（﹣1，2）关于直线x=1的对称点的坐标为．

查看试题解析
13. 如图，∠C＝∠D＝90º，添加一个条件： (写出一个条件即可)，可使 Rt△ABC 与Rt△ABD 全等．

查看试题解析
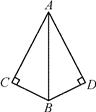14. 已知点 M(4－2t ， t－5)，若点 M 在 x 轴的下方、y 轴的右侧，则 t 的取值范围是．

查看试题解析
15. 如图，已知 l₁∥l₂∥l₃ ，相邻两条平行直线间的距离为 1cm，若等腰直角三角形 ABC 的直角顶点 C 在l₁上，另两个顶点 A、B 分别在l₁、l₂上，则 AB 的长是．

查看试题解析
16. 如图，已知直线 y= $- \frac{3}{4}$ x＋3 与 x 轴、y 轴分别交于点 A、B ，线段 AB 为直角边在第一内作等腰 Rt△ABC ， ∠BAC＝90º．点 P 是 x 轴上的一个动点，设 P(x ， 0)．

(1)、当 x ＝时，PB＋PC 的值最小；

(2)、当 x ＝时，|PB－PC|的值最大．

查看试题解析

三、解答题

17. 已知：如图，点 E ， F 在 BC 上，BE＝CF ， ∠A＝∠D ， ∠BED＝∠AFC ， AF 与 DE交于点 O ．
求证：OA＝OD ．

查看试题解析
18. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价是2100元/台；B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的利润不低于116000元,求A型号家用净水器最多能购进多少台?(注:利润=售价-进价)

查看试题解析
19. 已知一次函数y＝kx＋4(k≠0)．

(1)、当 x＝－1 时，y＝2，求此函数的表达式；

(2)、函数图象与 x 轴、y 轴的交点分别为 A、B，求出△AOB 的面积；

(3)、利用图象求出当y≤3时，x的取值范围．

查看试题解析
20. 如图，平面直角坐标系 xOy 中，已知点 A(0，3)，点 B( $\sqrt{3}$ ，0)，连接 AB ．若对于平面内一点 C ，当△ABC 是以 AB 为腰的等腰三角形时，称点 C 是线段 AB 的“等长点”

(1)、在点 C1 (－2， $3 + 2 \sqrt{2}$ )，点 C2 (0，－2)，点 C3 ( $3 + \sqrt{3}$ ， $- \sqrt{3}$ )中，线段 AB 的“等长点”是点；

(2)、若点 D( m ， n )是线段 AB 的“等长点”，且∠DAB＝60º，求 m 和 n 的值．

查看试题解析
21. 在直线上顺次取A，B，C三点，分别以AB，BC为边长在直线的同侧作正三角形，作得两个正三角形的另一顶点分别为D，E．

(1)、如图①，连结CD，AE，求证：CD=AE；

(2)、如图②，若AB=1，BC=2，求DE的长；

(3)、如图③，将图②中的正三角形BEC绕B点作适当的旋转，连结AE，若有DE²+BE²=AE² ，试求∠DEB的度数．

查看试题解析
22. 如图①，已知直线y＝﹣2x+4与x轴、y轴分别交于点A、C ，以OA、OC为边在第一象限内作长方形OABC ．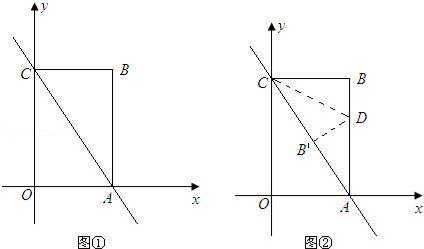

(1)、求点A、C的坐标；

(2)、将△ABC对折，使得点A的与点C重合，折痕交AB于点D ，求直线CD的解析式（图②）；

(3)、在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析