2016-2017学年四川省成都市彭州市五校联考高二下学期期中数学试卷（文科）

试卷更新日期：2017-07-25 类型：期中考试

进入出卷网下载

一、选择题

1. 已知集合U=R，Q={x|﹣2≤x≤3}，P={x|x﹣2＜0}，则Q∩（∁_UP）=（）

A、{x|1≤x≤2} B、{x|x≥1} C、{x|1＜x≤2} D、{x|2≤x≤3}

查看试题解析
2. 若复数Z满足Z（i﹣1）=2i（i为虚数单位），则 $\bar{z}$ 为（）

A、1+i B、1﹣i C、﹣1+i D、﹣1﹣i

查看试题解析
3. 已知向量 $\vec{a}$ =（k，3）， $\vec{b}$ =（1，4）， $\vec{c}$ =（2，1）且（2 $\vec{a}$ ﹣3 $\vec{b}$ ）⊥ $\vec{c}$ ，则实数k=（）

A、﹣ $\frac{9}{2}$ B、0 C、3 D、 $\frac{15}{2}$

查看试题解析
4. 设a，b∈R，则“a≥1且b≥1”是“a+b≥2”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 执行如图所示的程序框图，则输出S=（）

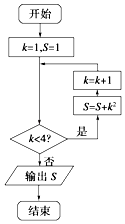A、2 B、6 C、15 D、31

查看试题解析
6. 关于函数f（x）=5sin3x+5 $\sqrt{3}$ cos3x，下列说法正确的是（）

A、函数f（x）关于x= $\frac{5}{9}$ π对称 B、函数f（x）向左平移 $\frac{π}{18}$ 个单位后是奇函数 C、函数f（x）关于点（ $\frac{π}{18}$ ，0）中心对称 D、函数f（x）在区间[0， $\frac{π}{20}$ ]上单调递增

查看试题解析
7. 某研究机构对儿童记忆能力x和识图能力y进行统计分析，得到如下数据：
记忆能力x
4
6
8
10
识图能力y
3
5
6
8
由表中数据，求得线性回归方程为 $\hat{y} = \frac{4}{5} x + \hat{a}$ ，若某儿童的记忆能力为12时，则他的识图能力为（）

A、9.2 B、9.5 C、9.8 D、10

查看试题解析
8. 若函数f（x）=kx﹣lnx在区间（1，+∞）单调递增，则k的取值范围是（）

A、（﹣∞，﹣2] B、（﹣∞，﹣1] C、[2，+∞） D、[1，+∞）

查看试题解析
9. 某几何体的三视图如图所示，且该几何体的体积是 $\frac{3}{2}$ ，则正视图中的x的值是（）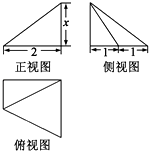

A、2 B、 $\frac{9}{2}$ C、 $\frac{3}{2}$ D、3

查看试题解析
10. 若直线mx+ny+2=0（m＞0，n＞0）截得圆（x+3）²+（y+1）²=1的弦长为2，则 $\frac{1}{m} + \frac{3}{n}$ 的最小值为（）

A、4 B、12 C、16 D、6

查看试题解析
11. 已知抛物线y²=2px（p＞0）的焦点为F，P、Q是抛物线上的两点，若△FPQ是边长为2的正三角形，则p的值是（）

A、 $2 \pm \sqrt{3}$ B、 $2 + \sqrt{3}$ C、 $\sqrt{3} \pm 1$ D、 $\sqrt{3} - 1$

查看试题解析
12. 已知f（x）是定义在R上且以2为周期的偶函数，当0≤x≤1，f（x）=x² ．如果函数g（x）=f（x）﹣（x+m）有两个零点，则实数m的值为（）

A、2k（k∈Z） B、2k或2k+ $\frac{1}{4}$ （k∈Z） C、0 D、2k或2k﹣ $\frac{1}{4}$ （k∈Z）

查看试题解析

二、填空题

13. 利用分层抽样的方法在学生总数为800的年级中抽取20名同学，其中女生人数为8人，则该年级男生人数为．

查看试题解析
14. 若x，y满足约束条件 ${\begin{matrix} y - x \leq 1 \\ x + y \leq 3 \\ y \geq 1 \end{matrix}$ ，则z=x+3y的最大值为．

查看试题解析
15. 已知等差数列{a_n}的前n项和为S_n ，若a₃+a₄=18﹣a₆﹣a₅ ，则S₈= ．

查看试题解析
16. 对任意实数x，[x]表示不超过x的最大整数，如[3.6]=3，[﹣3.6]=﹣4，关于函数f（x）=[ $\frac{x + 1}{3}$ ﹣[ $\frac{x}{3}$ ]]，有下列命题：
①f（x）是周期函数；
②f（x）是偶函数；
③函数f（x）的值域为{0，1}；
④函数g（x）=f（x）﹣cosπx在区间（0，π）内有两个不同的零点，
其中正确的命题为（把正确答案的序号填在横线上）．

查看试题解析

三、解答题：

17. 设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，且a=2bsin A．
（Ⅰ）求角B的大小；
（Ⅱ）若a= $3 \sqrt{3}$ ，c=5，求△ABC的面积及b．

查看试题解析
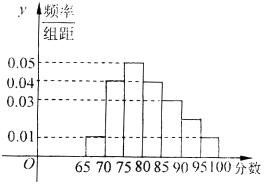
18. 如图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80～90分数段的学员数为21人．
（Ⅰ）求该专业毕业总人数N和90～95分数段内的人数n；
（Ⅱ）现欲将90～95分数段内的n名人分配到几所学校，从中安排2人到甲学校去，若n人中仅有两名男生，求安排结果至少有一名男生的概率．

查看试题解析
19. 如图，直四棱柱ABCD﹣A₁B₁C₁D₁中，AB∥CD，AD⊥AB，AB=2，AD= $\sqrt{2}$ ，AA₁=3，E为CD上一点，DE=1，EC=3

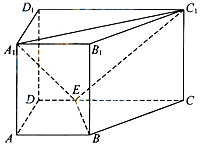(1)、证明：BE⊥平面BB₁C₁C；

(2)、求三棱锥B₁﹣EA₁C₁的体积．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的焦距为4 $\sqrt{3}$ ，且椭圆C过点（2 $\sqrt{3}$ ，1）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设椭圆C与y轴负半轴的交点为B，如果直线y=kx+1（k≠0）交椭圆C于不同的两点E、F，且B，E，F构成以EF为底边，B为顶点的等腰三角形，判断直线EF与圆x²+y²= $\frac{1}{2}$ 的位置关系．

查看试题解析
21. 已知函数f（x）=e^x ， g（x）=mx²+ax+b，其中m，a，b∈R，e=2.71828…为自然对数的底数．
（I）函数h（x）=xf （x），当a=l，b=0时，若函数h（x）与g（x）具有相同的单调区间，求m的值；
（II）记F（x）=f（x）﹣g（x）．当a=2，m=0时，若函数F（x）在[﹣1，2]上存在两个不同的零点，求b的取值范围．

查看试题解析
22. 在直角坐标系xOy中，直线l的参数方程为 ${\begin{matrix} x = 3 + \frac{1}{2} t \\ y = \frac{\sqrt{3}}{2} t \end{matrix}$ （t为参数），以原点为极点，x轴正半轴为极轴建立极坐标系，⊙C的极坐标方程为ρ=2 $\sqrt{3}$ sinθ．
（Ⅰ）写出⊙C的直角坐标方程；
（Ⅱ）P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．

查看试题解析

记忆能力x	4	6	8	10
识图能力y	3	5	6	8