2016-2017学年四川省成都市九校联考高二下学期期中数学试卷（文科）

试卷更新日期：2017-07-25 类型：期中考试

进入出卷网下载

一、选择题

1. 在复平面内，复数 z=3+4i 则 z 的共轭复数的模为（）

A、3 B、4 C、5 D、25

查看试题解析
2. 函数 f （ x）=sin x+e^x ，则 f'（0）的值为（）

A、1 B、2 C、3 D、0

查看试题解析
3. 已知m，n表示两条不同直线，α表示平面，下列说法正确的是（　　）

A、若m∥α，n∥α，则m∥n B、若m⊥α，n⊂α，则m⊥n C、若m⊥α，m⊥n，则n∥α D、若m∥α，m⊥n，则n⊥α

查看试题解析
4. 已知a为函数f（x）=x³﹣3x的极小值点，则a=（）

A、﹣1 B、﹣2 C、2 D、1

查看试题解析
5. 函数 f （ x）= $\frac{x}{l n x}$ （ x＞1）单调递减区间是（）

A、（1，+∞） B、（1，e²） C、（e，+∞） D、（1，e）

查看试题解析
6. 为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区 5 户家庭，得到如下统计数据表：
收入 x （万元）
8.2
8.6
10.0
11.3
11.9
支出 y （万元）
6.2
7.5
8.0
8.5
9.8
根据上表可得回归直线方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ ，其中 $\hat{b}$ =0.76， $\hat{a}$ =y﹣ $\hat{b}$ x，据此估计，该社区一户收入为 14 万元家庭年支出为（）

A、11.04 万元 B、11.08 万元 C、12.12 万元 D、12.02 万元

查看试题解析
7. 函数f（x）= $\frac{x}{2}$ +cosx，x∈[0， $\frac{π}{2}$ ]的最大值是（）

A、1 B、 $\frac{π}{4}$ C、 $\frac{π}{12}$ + $\frac{\sqrt{3}}{2}$ D、 $\frac{π}{6}$ + $\frac{1}{2}$

查看试题解析
8. 某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x的值是（）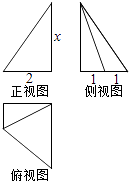

A、2 B、 $\frac{9}{2}$ C、 $\frac{3}{2}$ D、3

查看试题解析
9. 若对任意的x＞0，恒有lnx≤px﹣1（p＞0），则p的取值范围是（）

A、（0，1] B、（1，+∞） C、（0，1） D、[1，+∞）

查看试题解析
10. 甲、乙两人约定在下午 4：30：5：00 间在某地相见，且他们在 4：30：5：00 之间到达的时刻是等可能的，约好当其中一人先到后一定要等另一人 20 分钟，若另一人仍不到则可以离去，则这两人能相见的概率是（）

A、 $\frac{3}{4}$ B、 $\frac{8}{9}$ C、 $\frac{7}{16}$ D、 $\frac{11}{12}$

查看试题解析
11. 已知 y=f （ x ）是定义在 R 上的偶函数，且当 x∈（﹣∞，0），f （ x ）+xf'（ x ）＜0成立（ f'（ x ）是函数 f （ x）的导数），若 a= $\frac{1}{2}$ f （log₂ $\sqrt{2}$ ），b=（ln 2 ） f （ln 2 ），c=2f （﹣2 ），则 a，b，c 的大小关系是（）

A、a＞b＞c B、b＞a＞c C、c＞a＞b D、a＞c＞b

查看试题解析
12. 已知F₁ ， F₂分别为双曲线C： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1的左、右焦点，若存在过F₁的直线分别交双曲线C的左、右支于A，B两点，使得∠BAF₂=∠BF₂F₁ ，则双曲线C的离心率e的取值范围是（）

A、（3，+∞） B、（1，2+ $\sqrt{5}$ ） C、（3，2+ $\sqrt{5}$ ） D、（1，3）

查看试题解析

二、填空题

13. 已知f（x）=axlnx+1，x∈（0，+∞）（a∈R），f′（x）为f（x）的导函数，
f′（1）=2，则a= ．

查看试题解析
14. 甲、乙两位学生参加数学文化知识竞赛培训．在培训期间，他们参加的 5 次测试成绩记录如下：甲：82
82 79 95 87 乙：95 75 80 90 85现要从甲、乙两位同学中选派一人参加正式比赛，从统计学的角度考虑，你认为选派同学参加合适．

查看试题解析
15. 已知椭圆 C₁： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）与双曲线 C₂：x²﹣y²=4 有相同的右焦点F₂ ，点P是C₁与C₂的一个公共点，若|PF₂|=2，则椭圆 C₁的离心率等于．

查看试题解析
16. 已知函数f（x）=ax³﹣3x²+1，若f（x）存在唯一的零点x₀ ，且x₀＜0，则a的取值范围是．

查看试题解析

三、解答题

17. 某校举行环保知识竞赛，为了了解本次竞赛成绩情况，从得分不低于50分的试卷中随机抽取100名学生的成绩（得分均为正数，满分100分），进行统计，请根据频率分布表中所提供的数据，解答下列问题：
（Ⅰ）求a、b的值；
（Ⅱ）若从成绩较好的第3、4、5组中，按分层抽样的方法抽取6人参加社区志愿者活动，并从中选出2人做负责人，求2人中至少有1人是第四组的概率．
组号
分组
频数
频率
第1组
[50，60]
5
0.05
第2组
[60，70]
a
0.35
第3组
[70，80]
30
b
第4组
[80，90]
20
0.20
第5组
[90，100]
10
0.10
合计
100
1.00

查看试题解析
18. 如图，在三棱柱ABC﹣A₁B₁C₁中侧棱垂直于底面，AC⊥BC，点D是AB的中点．求证：
（Ⅰ） AC⊥BC₁；
（Ⅱ） AC₁∥平面 B₁CD；
（Ⅲ）若 AC=BC=1，AA₁=2，求三棱锥DB₁BC的体积．

查看试题解析
19. 2016年1月1日起全国统一实施全面两孩政策．为了解适龄民众对放开生育二胎政策的态度，某市选取70后和80后作为调查对象，随机调查了100位，得到数据如表：
生二胎
不生二胎
合计
70后
30
15
45
80后
45
10
55
合计
75
25
100
（Ⅰ）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若从该市70后公民中随机抽取3位，记其中生二胎的人数为X，求随机变量X的分布列和数学期望；
（Ⅱ）根据调查数据，是否有90%以上的把握认为“生二胎与年龄有关”，并说明理由．
参考数据：
P（K²＞k）
0.15
0.10
0.05
0.025
0.010
0.005
k
2.072
2.706
3.841
5.024
6.635
7.879
（参考公式： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d）

查看试题解析
20. 已知函数f（x）=x²+2alnx．
（Ⅰ）若函数f（x）的图象在（2，f（2））处的切线斜率为1，求实数a的值；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）若函数 $g (x) = \frac{2}{x} + f (x)$ 在[1，2]上是减函数，求实数a的取值范围．

查看试题解析
21. 已知椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0 ）经过点 P（1， $\frac{\sqrt{2}}{2}$ ），离心率 e= $\frac{\sqrt{2}}{2}$ ．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）设过点E （0，﹣2 ）的直线l与C相交于P，Q 两点，求△OPQ面积的最大值．

查看试题解析
22. 已知函数g（ x）=e ^x+ $\frac{a}{2}$ x² ，其中a∈R，e=2.71828…为自然对数的底数，f （ x）是 g（ x）的导函数．
（Ⅰ）求 f（ x）的极值；
（Ⅱ）若a=﹣1，证明：当 x₁≠x₂ ，且f （ x₁ ）=f （ x₂）时，x₁+x₂＜0．

查看试题解析

收入 x （万元）	8.2	8.6	10.0	11.3	11.9
支出 y （万元）	6.2	7.5	8.0	8.5	9.8

组号	分组	频数	频率
第1组	[50，60]	5	0.05
第2组	[60，70]	a	0.35
第3组	[70，80]	30	b
第4组	[80，90]	20	0.20
第5组	[90，100]	10	0.10
合计		100	1.00

	生二胎	不生二胎	合计
70后	30	15	45
80后	45	10	55
合计	75	25	100

P（K²＞k）	0.15	0.10	0.05	0.025	0.010	0.005
k	2.072	2.706	3.841	5.024	6.635	7.879