2016-2017学年山东省潍坊市四县市联考高二下学期期中数学试卷（文科）

试卷更新日期：2017-07-25 类型：期中考试

进入出卷网下载

一、选择题

1. 若复数z=3﹣2i，则z的共轭复数 $\bar{z}$ （）

A、﹣3+2i B、﹣3﹣2i C、﹣2+3i D、3+2i

查看试题解析
2. 用反证法证明命题“设a，b为实数，则方程x³+ax+b=0至少有一个实根”时，要做的假设是（　　）

A、方程^{$x^{3}$}+ax+b=0没有实根 B、方程^{$x^{3}$}+ax+b=0至多有一个实根 C、方程^{$x^{3}$}+ax+b=0至多有两个实根 D、方程^{$x^{3}$}+ax+b=0恰好有两个实根

查看试题解析
3. 已知函数y=f（x），下列说法错误的是（）

A、△y=f（x₀+△x）﹣f（x₀）叫函数增量 B、 $\frac{△ y}{△ x} = \frac{f (x_{0} + △ x) - f (x_{0})}{△ x}$ 叫函数在[x₀ ， x₀+△x]上的平均变化率 C、f（x）在点x₀处的导数记为y′ D、f（x）在点x₀处的导数记为f′（x₀）

查看试题解析
4. 以下说法错误的是（）

A、推理一般分为合情推理和演绎推理 B、归纳是从特殊到一般的过程，它属于合情推理 C、在数学中，证明命题的正确性既能用演绎推理又能用合情推理 D、演绎推理经常使用的是由大前提、小前提得到结论的三段论推理

查看试题解析
5. 某产品的广告费用x（万元）与销售额y（万元）的统计数据如表：
广告费x（万元）
3
4
5
6
销售额y（万元）
25
30
40
45
根据表可得回归直线方程 $\hat{y}$ =7x+ $\hat{a}$ ，若广告费用为10万元，则预计销售额为（）

A、73万元 B、73.5万元 C、74万元 D、74.5万元

查看试题解析
6. 某品牌电动汽车的耗电量y与速度x之间满足的关系式为y= $\frac{1}{3}$ x³﹣ $\frac{39}{2}$ x²﹣40x（x＞0），为使耗电量最小，则速度为（）

A、30 B、40 C、50 D、60

查看试题解析
7. 以下式子正确的个数是（）
①（ $\frac{1}{x}$ ）′= $\frac{1}{x^{2}}$ ②（cosx）′=﹣sinx ③（2^x）′=2^xln2 ④（lgx）′= $\frac{- 1}{x l n 10}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知函数f（x）=lnx+x，则曲线f（x）在点P（1，f（1））处的切线与两坐标轴围成的三角形的面积为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
9. 甲、乙、丙三位同学被问到是否去过济南、潍坊、青岛三个城市时，甲说：我去过的城市比乙多，但没去过潍坊；乙说：我没去过青岛；丙说：我们三人去过同一城市；由此可判断乙去过的城市为（）

A、济南 B、青岛 C、济南和潍坊 D、济南和青岛

查看试题解析
10. 函数f（x）的定义域为R，导函数f'（x）的图象如图所示，则函数f（x）（）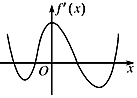

A、无极大值点，有四个极小值点 B、有三个极大值点，两个极小值点 C、有两个极大值点，两个极小值点 D、有四个极大值点，无极小值点

查看试题解析
11. 古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”，而把1、4、9、16、25、…这样的数称为“正方形数”．从如图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式中，符合这一规律的是（）

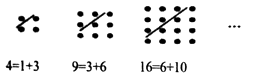A、16=3+13 B、25=9+16 C、36=10+26 D、49=21+28

查看试题解析
12. 已知函数f（x）=asinx+bx³+1（a，b∈R），f′（x）为f（x）的导函数，则f（2016）+f（﹣2016）+f′（2017）﹣f′（﹣2017）=（）

A、2017 B、2016 C、2 D、0

查看试题解析

二、填空题

13. 已知m为函数f（x）=x³﹣12x的极大值点，则m= ．

查看试题解析
14. 已知圆的方程式x²+y²=r² ，经过圆上一点M（x₀ ， y₀）的切线方程为x₀x+y₀y=r² ，类别上述方法可以得到椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 类似的性质为：经过椭圆上一点M（x₀ ， y₀）的切线方程为．

查看试题解析
15. 欧拉公式e^xi=cosx+isinx（i为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知，e³ⁱ表示的复数在复平面中位于象限．

查看试题解析
16. 对于函数f（x）=xlnx有如下结论：
①该函数为偶函数；
②若f′（x₀）=2，则x₀=e；
③其单调递增区间是[ $\frac{1}{e}$ ，+∞）；
④值域是[ $\frac{1}{e}$ ，+∞）；
⑤该函数的图象与直线y=﹣ $\frac{1}{e}$ 有且只有一个公共点．（本题中e是自然对数的底数）
其中正确的是（请把正确结论的序号填在横线上）

查看试题解析

三、解答题

17. 已知f（x）=lnx+ $\frac{1}{8}$ x² ．

(1)、求曲线f（x）在x=1处的切线方程；

(2)、设P为曲线f（x）上的点，求曲线C在点P处切线的斜率的最小值及倾斜角α的取值范围．

查看试题解析
18. 为了解少年儿童的肥胖是否与常喝碳酸饮料有关，现对100名六年级学生进行了问卷调查得到如图联表．且平均每天喝500ml以上为常喝，体重超过50kg为肥胖．已知在全部100人中随机抽取1人，抽到肥胖的学生的概率为0.8．
常喝
不常喝
合计
肥胖
60
不肥胖
10
合计
100

(1)、求肥胖学生的人数并将上面的列联表补充完整；

(2)、是否有95%的把握认为肥胖与常喝碳酸饮料有关？说明你的理由．
附：参考公式：x²= $\frac{n {(n_{11} n_{22} - n_{12} n_{21})}^{2}}{n_{1 +} n_{2 +} n_{+ 1} n_{+ 2}}$
P（x²≥x₀）
0.05
0.025
0.010
0.005
0.001
x₀
3.841
5.024
6.635
7.879
10.828

查看试题解析
19. 综合题。

(1)、已知ABCD是复平面内的平行四边形，并且A，B，C三点对应的复数分别是3+i，﹣2i，﹣1﹣i，求D点对应的复数；

(2)、已知复数Z₁=2， $\frac{Z_{2}}{Z_{1}}$ =i，并且|z|=2 $\sqrt{2}$ ，|z﹣z₁|=|z﹣z₂|，求z．

查看试题解析
20. 已知函数f（x）= $\frac{e^{x + b}}{x}$ 过点（1，e）．

(1)、求y=f（x）的单调区间；

(2)、当x＞0时，求 $\frac{f (x)}{x}$ 的最小值；

(3)、试判断方程f（x）﹣mx=0（m∈R且m为常数）的根的个数．

查看试题解析
21. 在直角坐标系xOy中，圆C的参数方程 ${\begin{matrix} x = 1 + c o s φ \\ y = s i n φ \end{matrix}$ （φ为参数），以原点O为极点，x轴的正半轴为极轴，建立极坐标系．

(1)、求圆C的普通方程和极坐标方程；

(2)、射线OM：θ= $\frac{π}{4}$ 与圆C的交于O、P两点，求P的极坐标．

查看试题解析
22. 设函数f（x）=|x﹣a|+3x，其中a＞0．
（Ⅰ）当a=1时，求不等式f（x）≥3x+2的解集
（Ⅱ）若不等式f（x）≤0的解集为{x|x≤﹣1}，求a的值．

查看试题解析
23. 在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴，建立极坐标系．已知曲线C₁： ${\begin{matrix} x = 4 + c o s t \\ y = - 3 + s i n t \end{matrix}$ （t为参数），C₂： ${\begin{matrix} x = 6 c o s θ \\ y = 2 s i n θ \end{matrix}$ （θ为参数）．
（Ⅰ）化C₁ ， C₂的方程为普通方程，并说明它们分别表示什么曲线；
（Ⅱ）若C₁上的点P对应的参数为t=﹣ $\frac{π}{2}$ ，Q为C₂上的动点，求线段PQ的中点M到直线C₃：ρcosθ﹣ $\sqrt{3}$ ρsinθ=8+2 $\sqrt{3}$ 距离的最小值．

查看试题解析
24. 已知不等式|x+2|+|x﹣2|＜18的解集为A．

(1)、求A；

(2)、若∀a，b∈A，x∈（0，+∞），不等式a+b＜x $+ \frac{4}{x}$ +m恒成立，求实数m的取值范围．

查看试题解析

P（x²≥x₀）	0.05	0.025	0.010	0.005	0.001
x₀	3.841	5.024	6.635	7.879	10.828

广告费x（万元）	3	4	5	6
销售额y（万元）	25	30	40	45

	常喝	不常喝	合计
肥胖	60
不肥胖		10
合计			100