浙江省温州市龙湾区2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-13 类型:期中考试
一、选择题(本题有10小题,每题4分,共40分)
-
1. 下列各式中, 是关于 的二次函数的是A、 B、 C、 D、2. 下列说法正确的是A、25人中至少有3人的出生月份相同 B、任意抛掷一枚均匀的1元硬币,若上一次正面朝上,则下一次一定反面朝上 C、天气预报说明天降水的概率为 ,则明天一定是晴天 D、任意抛掷一枚均匀的骰子,掷出的点数小于3的概率是3. 如图所示是一个旋转对称图形,若将它绕自身中心旋转一定角度之后不能与原图重合,则这个角度可能是
 A、 B、 C、 D、4. 抛物线 与坐标轴的交点个数是A、0 B、1 C、2 D、35. 在一个不透明的箱子中有3张红卡和若干张绿卡,它们除了颜色外其他完全相同,通过多次抽卡试验后发现,抽到绿卡的概率稳定在 附近,则箱中卡的总张数可能是A、1张 B、4张 C、9张 D、12张6. 现有如下4个命题:
A、 B、 C、 D、4. 抛物线 与坐标轴的交点个数是A、0 B、1 C、2 D、35. 在一个不透明的箱子中有3张红卡和若干张绿卡,它们除了颜色外其他完全相同,通过多次抽卡试验后发现,抽到绿卡的概率稳定在 附近,则箱中卡的总张数可能是A、1张 B、4张 C、9张 D、12张6. 现有如下4个命题:①过两点可以作无数个圆.②三点可以确定一个圆.③任意一个三角形有且只有一个外接圆.④任意一个圆有且只有一个内接三角形.其中正确的有
A、1个 B、2个 C、3个 D、4个7. 如图,抛物线 的对称轴是直线 ,则下列结论正确的是 A、 B、 C、 D、8. 同一平面内,一个点到圆的最小距离为 ,最大距离为 ,则该圆的半径为A、 B、 C、 或 D、 或9. 《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )
A、 B、 C、 D、8. 同一平面内,一个点到圆的最小距离为 ,最大距离为 ,则该圆的半径为A、 B、 C、 或 D、 或9. 《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )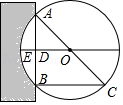 A、13寸 B、20寸 C、26寸 D、28寸10. 如图,在▱ABCD中,AB=6,BC=10,AB⊥AC,点P从点B出发沿着B→A→C的路径运动,同时点Q从点A出发沿着A→C→D的路径以相同的速度运动,当点P到达点C时,点Q随之停止运动,设点P运动的路程为x,y=PQ2 , 下列图象中大致反映y与x之间的函数关系的是( )
A、13寸 B、20寸 C、26寸 D、28寸10. 如图,在▱ABCD中,AB=6,BC=10,AB⊥AC,点P从点B出发沿着B→A→C的路径运动,同时点Q从点A出发沿着A→C→D的路径以相同的速度运动,当点P到达点C时,点Q随之停止运动,设点P运动的路程为x,y=PQ2 , 下列图象中大致反映y与x之间的函数关系的是( ) A、
A、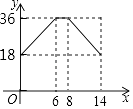 B、
B、 C、
C、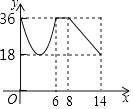 D、
D、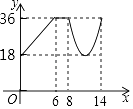
二、填空题(本题有6小题,每小题5分,共30分)
-
11. 二次函数 经过 和 ,则当 时,函数取到最小值.12. 一个口袋中放有除颜色外,形状大小都相同的黑白两种球,黑球6个,白球10个.现在往袋中放入 个白球和4个黑球,使得摸到白球的概率为 ,则 .13. 已知 的半径为2, 中有两条平行的弦 和 , , ,则两条弦之间的距离为 .14. 在平面直角坐标系中有 , , 三点, , , .现在要画一个圆同时经过这三点,则圆心坐标为 .15. 如图,边长为2的正方形 的顶点 、 在一个半径为2的圆上,顶点 、 在该圆内.将正方形 绕点 逆时针旋转,当点 第一次落在圆上时,点 旋转到 ,则 .
 16. 如图,抛物线 与反比例函数 的图象相交于点 ,且点 的横坐标为5,抛物线与 轴交于点 , 是抛物线的顶点, 和 分别是 轴和 轴上的两个动点,则 的最小值为 .
16. 如图,抛物线 与反比例函数 的图象相交于点 ,且点 的横坐标为5,抛物线与 轴交于点 , 是抛物线的顶点, 和 分别是 轴和 轴上的两个动点,则 的最小值为 .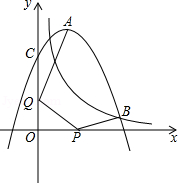
三、解答题(本题有8小题,共80分)
-
17. 如图,二次函数 的图象与 轴交于 、 两点,与 轴交于点 ,其中 ,
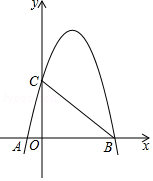 (1)、求二次函数的解析式,并求出当 时的函数值.(2)、连接 , ,得到 ,现将抛物线图象只向下平移 个单位,使得顶点落在 内部(不包括边界),请写出 的取值范围.18. 今年第18号台风“米娜”于10月1号上午出现在温州附近海域.如图,台风“米娜”的中心位于点 处,周围 都会受到台风影响.现在台风正往南偏东 的方向移动,在 的正南方 出有一座小镇 .在台风移动过程中,小镇 是否会受到影响,判断并说明理由.
(1)、求二次函数的解析式,并求出当 时的函数值.(2)、连接 , ,得到 ,现将抛物线图象只向下平移 个单位,使得顶点落在 内部(不包括边界),请写出 的取值范围.18. 今年第18号台风“米娜”于10月1号上午出现在温州附近海域.如图,台风“米娜”的中心位于点 处,周围 都会受到台风影响.现在台风正往南偏东 的方向移动,在 的正南方 出有一座小镇 .在台风移动过程中,小镇 是否会受到影响,判断并说明理由. 19. 学校组织了一次迷宫探险活动.经过迷宫中的某一处路口时,我们可能继续直行,也可能向左转或向右转,这三种可能性大小相同.现有甲、乙两位同学先后经过这一处路口.(1)、请用“列表法”或画“树状图法”写出两人经过该路口时的所有行走情况.(2)、假设在路口的左边有陷阱,求出陷阱被触发的概率.20. 如图,已知
19. 学校组织了一次迷宫探险活动.经过迷宫中的某一处路口时,我们可能继续直行,也可能向左转或向右转,这三种可能性大小相同.现有甲、乙两位同学先后经过这一处路口.(1)、请用“列表法”或画“树状图法”写出两人经过该路口时的所有行走情况.(2)、假设在路口的左边有陷阱,求出陷阱被触发的概率.20. 如图,已知 (1)、用直尺和圆规作出 ,使 经过 、 两点,且圆心 在 边上.(不写作法,保留作图痕迹)(2)、若 , , 的半径2,求 的长.21. 已知函数(1)、判断该函数的图象与 轴的交点个数.(2)、若 ,求出函数值 在 时的取值范围.(3)、若方程 在 内有且只有一个解,直接写出 的范围.22. 如图,在等腰 中, , 是 的外接圆, , .
(1)、用直尺和圆规作出 ,使 经过 、 两点,且圆心 在 边上.(不写作法,保留作图痕迹)(2)、若 , , 的半径2,求 的长.21. 已知函数(1)、判断该函数的图象与 轴的交点个数.(2)、若 ,求出函数值 在 时的取值范围.(3)、若方程 在 内有且只有一个解,直接写出 的范围.22. 如图,在等腰 中, , 是 的外接圆, , . (1)、求出 的半径 .(2)、求 .23. 某旅馆一共有客房30间,在国庆期间,老板通过观察记录发现,当所有房间都有旅客入住时,每间客房净赚600元,客房价格每提高50元,则会少租出去1个房间.同时没有旅客入住的房间,需要花费50元来进行卫生打理.(1)、求出每天利润 的最大值,并求出利润最大时,有多少间客房入住了旅客.(2)、若老板希望每天的利润不低于19500元,且租出去的客房数量最少,求出此时每间客房的利润.24. 如图,在平面直角坐标系中,抛物线 交 轴于点 ,交 轴于点 和点 ,过点 作 轴交抛物线于点 .
(1)、求出 的半径 .(2)、求 .23. 某旅馆一共有客房30间,在国庆期间,老板通过观察记录发现,当所有房间都有旅客入住时,每间客房净赚600元,客房价格每提高50元,则会少租出去1个房间.同时没有旅客入住的房间,需要花费50元来进行卫生打理.(1)、求出每天利润 的最大值,并求出利润最大时,有多少间客房入住了旅客.(2)、若老板希望每天的利润不低于19500元,且租出去的客房数量最少,求出此时每间客房的利润.24. 如图,在平面直角坐标系中,抛物线 交 轴于点 ,交 轴于点 和点 ,过点 作 轴交抛物线于点 . (1)、求此抛物线的表达式;(2)、点 是抛物线上一点,且点 关于 轴的对称点在直线 上,求 的面积;(3)、若点 是直线 下方的抛物线上一动点,当点 运动到某一位置时, 的面积最大,求出此时点 的坐标和 的最大面积.
(1)、求此抛物线的表达式;(2)、点 是抛物线上一点,且点 关于 轴的对称点在直线 上,求 的面积;(3)、若点 是直线 下方的抛物线上一动点,当点 运动到某一位置时, 的面积最大,求出此时点 的坐标和 的最大面积.