浙江省宁波市余姚市、海曙区2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2019-12-13 类型：期中考试

进入出卷网下载

一、选择题（每小题2分，共24分）

1. 如果+3吨表示运入仓库的大米吨数，那么运出5吨大米表示为

A、－5吨 B、+5吨 C、－3吨 D、+3吨

查看试题解析
2. 下列化简正确的是（）

A、 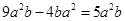$8 x - 7 y = x y$ B、 $a^{2} b - 2 a b^{2} = - a b^{2}$ C、 D、 $5 m - 4 m = 1$

查看试题解析
3. 一周时间有604800秒，604800用科学记数法表示为（）

A、 $6048 \times 10^{2}$ B、 $6.048 \times 10^{5}$ C、 $6.048 \times 10^{6}$ D、 $0.6048 \times 10^{6}$

查看试题解析
4. $2 x - (3 x^{2} + 4 x)$ 的化简结果是（）

A、 $9 x^{2}$ B、 $24 x^{4}$ C、 $3 x^{2} + 6 x$ D、 $- 3 x^{2} - 2 x$

查看试题解析
5. 下列说法正确的是（）

A、 $\sqrt{81}$ 的平方根是3 B、（－1）²⁰¹⁰是最小的自然数 C、两个无理数的和一定是无理数 D、实数与数轴上的点一一对应

查看试题解析
6. 如图，组成正方形网格的小正方形边长为1，那么点A表示的数为（）

A、 $\sqrt{10}$ B、 $\sqrt{11}$ C、 $\sqrt{12}$ D、 $\sqrt{13}$

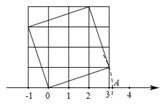查看试题解析
7. 有20筐白菜，以每筐30千克为标准，超过或不足的分别用正、负来表示，记录如表：

与标准质量的差（单位：千克）

﹣3

﹣2

﹣0.5

0

2.5

筐数

1

4

2

5

8

则这20筐白菜的总重量为（）

A、710千克 B、608千克 C、615千克 D、596千克

查看试题解析
8. 如果代数式 $x - 2 y - 2$ 的值为 $- 1$ ，那么代数式 $6 - 2 x + 4 y$ 的值为（）

A、0 B、2 C、-2 D、4

查看试题解析
9. 由下表可得 $\sqrt{7}$ 精确到百分位的近似数是（）

A、2.64 B、2.65 C、2.7 D、2.646

查看试题解析
10. 按如图所示的运算程序，能使输出的结果为3的是（）

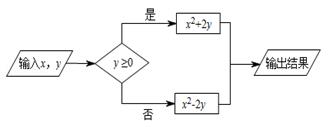A、x＝1，y＝2 B、x＝﹣2，y＝﹣2 C、x＝3，y＝1 D、x＝﹣1，y＝﹣1

查看试题解析
11. 张师傅下岗后做起了小生意，第一次进货时，他以每件a元的价格购进了20件甲种小商品，以每件b元的价格购进了30件乙种小商品（a>b）．根据市场行情，他将这两种小商品都以 $\frac{a + b}{2}$ 元的价格出售．在这次买卖中，张师傅的盈亏状况为（）

A、赚了（25a+25b）元 B、亏了（20a+30b）元 C、赚了（5a-5b）元 D、亏了（5a-5b）元

查看试题解析
12. 一个自然数若能表示为两个自然数的平方差，则称这个自然数为“智慧数”，比如99=10²-1² ，故99是一个智慧数．在下列各数中，不属于“智慧数”的是（）

A、15 B、16 C、17 D、18

查看试题解析

二、填空题（每题4分，共24分）

13. 比较大小：

(1)、2 $| - \frac{5}{2} |$ ；

(2)、－70；

(3)、 $- \frac{2}{3}$ $- \frac{3}{4}$ ；

(4)、 $- | - 2.7 |$ $- 2 \frac{2}{3}$ ．

查看试题解析
14. 和式 $\frac{2}{3} - 1 \frac{1}{2} - 1 \frac{1}{3} + 4$ 中第3个加数是，该和式的运算结果是．

查看试题解析
15. 把下列各数填入相应的横线上：
－2，2π， $- \frac{3}{5}$ ，0，－3.7， $\sqrt{16}$ ，0.35， $\sqrt[3]{9}$

整数：；正有理数：；

无理数：；负分数：．

查看试题解析
16. $- \frac{3 x y^{3}}{7}$ 的系数是，次数是； $4 a^{3} - a^{2} b^{2} - \frac{4}{3} a b$ 是次项式．

查看试题解析
17. 如图，数轴的单位长度为1，当点B为原点时，若存在一点M到A的距离是点M到D 的距离的2倍，则点M所表示的数是．

查看试题解析
18. 如图是由从1开始的连续自然数组成，则第8行第8 个数是，第n 行第一个数可表示为．

查看试题解析

三、解答题（第19题12分，第20~23题各6分，第24~25题8分，共52分）

19.

(1)、－5－(－4)+7－8

(2)、 $3 \frac{1}{2}$ ÷（－35）× $\frac{1}{5}$

(3)、 $- 2^{4} - \sqrt{36} + 6 \div (- \frac{2}{3}) \times \sqrt[3]{- 8}$

(4)、 $(- 5) \times (- 3 \frac{2}{5}) + (- 7) \times 3 \frac{2}{5} - 12 \times (- 3 \frac{2}{5})$

查看试题解析
20. 化简：

(1)、 $2 x + 1 - 7 x - 2$

(2)、 $3 （ x^{2} - \frac{1}{2} y^{2}) - \frac{1}{2} (4 x^{2} - 3 y^{2})$

查看试题解析
21. 把下列各数在数轴上表示出来，并把它们按从小到大的顺序用“＜”连接起来：
3 $\frac{1}{2}$ ，﹣2.5，|﹣2|，0， $\sqrt[3]{- 8}$ ，（﹣1）² ．

查看试题解析
22. 已知 $| a - 1 | + {(b + 2)}^{2} = 0$ ，求多项式 $3 ab - 15 b^{2} + 5 a^{2} - 6 ba + 15 a^{2} - 2 b^{2}$ 的值.

查看试题解析
23. 一个正方体的体积是125cm³ ，现将它锯成8块同样大小的正方体小木块.

(1)、求每个小正方体的棱长.

(2)、现有一张面积为36 cm²长方形木板，已知长方形的长是宽的4倍，若把以上小正方体排放在这张长方形木板上，且只排放一层，最多可以放几个小正方体？请说明理由.

查看试题解析
24. “湖田十月清霜堕，晚稻初香蟹如虎”，又到了食蟹的好季节啦！某经销商去水产批发市场采购太湖蟹，他看中了A、B两家的某种品质相近的太湖蟹．零售价都为60元／千克，批发价各不相同．
A家规定：批发数量不超过100千克，按零售价的92%优惠；批发数量超过100千克但不超过200千克，按零售价的90%优惠；超过200千克的按零售价的88%优惠．
B家的规定如下表：
数量范围（千克）
0～50
部分
50以上～150
部分
150以上～250
部分
250以上
部分
价格（元）
零售价的95%
零售价的85%
零售价的75%
零售价的70%

(1)、如果他批发80千克太湖蟹，则他在A 、B两家批发分别需要多少元？

(2)、如果他批发x千克太湖蟹 (150＜x＜200)，请你分别用含字母x的式子表示他在A 、B两家批发所需的费用；

(3)、现在他要批发195千克太湖蟹，你能帮助他选择在哪家批发更优惠吗？请说明理由．

查看试题解析
25. 在一条不完整的数轴上从左到右有点A，B，D，C，其中AB＝2，BD＝3，DC＝1，如图所示，设点A，B，D，C所对应数的和是p ．

(1)、若以B为原点．写出点A，D，C所对应的数，并计算p的值；

(2)、若原点O在图中数轴上点C的右边，且CO＝x ， p＝﹣71，求x的值．

查看试题解析

四、附加题（第26，27题各5分，共10分）

26. 已知 $| x + y - 3 | = - 2 x - 2 y$ ，求 ${(x + y)}^{3}$ 的值．

查看试题解析
27. 如图，它是由A、B、E、F四个正方形，C、D两个长方形拼成的大长方形，已知正方形F的边长为6，求拼成的大长方形周长．

查看试题解析

与标准质量的差（单位：千克）	﹣3	﹣2	﹣0.5	0	2.5
筐数	1	4	2	5	8