2017年山东省枣庄市薛城区中考数学模拟试卷（5月份）

试卷更新日期：2017-07-25 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、a³+a²=2a⁵ B、2a（1﹣a）=2a﹣2a² C、（﹣ab²）³=a³b⁶ D、（a+b）²=a²+b²

查看试题解析
2. 习近平总书记提出了未来5年“精准扶贫”的战略构想，意味着每年要减贫约11700000人，将数据11700000用科学记数法表示为（）

A、1.17×10⁶ B、1.17×10⁷ C、1.17×10⁸ D、11.7×10⁶

查看试题解析
3. 如图，直线a∥b，∠1=85°，∠2=35°，则∠3=（）

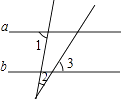A、85° B、60° C、50° D、35°

查看试题解析
4. 在一次数学测试中，某学习小组6名同学的成绩（单位：分）分别为65，82，86，82，76，95．关于这组数据，下列说法错误的是（）

A、众数是82 B、中位数是82 C、极差是30 D、平均数是82

查看试题解析
5.
如图，若要添加一条线段，使之既是轴对称图形又是中心对称图形，正确的添加位置是（）

A、 B、 C、 D、

查看试题解析
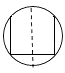6.
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（）

A、（ $\sqrt{3}$ ，﹣1） B、（1，﹣ $\sqrt{3}$ ） C、（ $\sqrt{2}$ ，﹣ $\sqrt{2}$ ） D、（﹣ $\sqrt{2}$ ， $\sqrt{2}$ ）

查看试题解析
7. 如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan∠ADE的值为（）

A、 $\frac{3}{2}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{2 \sqrt{13}}{13}$

查看试题解析
8. 如图，已知AC是⊙O的直径，点B在圆周上（不与A、C重合），点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB=3∠ADB，则（）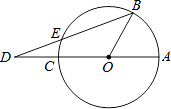

A、DE=EB B、 $\sqrt{2}$ DE=EB C、 $\sqrt{3}$ DE=DO D、DE=OB

查看试题解析
9. 如图，在平面直角坐标系中，点P（1，4）、Q（m，n）在函数y= $\frac{k}{x}$ （x＞0）的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C、D．QD交PA于点E，随着m的增大，四边形ACQE的面积（）

A、减小 B、增大 C、先减小后增大 D、先增大后减小

查看试题解析
10. 如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（）

A、 $\frac{8 \sqrt{3}}{5}$ B、2 $\sqrt{2}$ C、 $\frac{14}{5}$ D、10﹣5 $\sqrt{2}$

查看试题解析
11. 如图是抛物线y=ax²+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间．则下列结论：
①a﹣b+c＞0；
②3a+b=0；
③b²=4a（c﹣n）；
④一元二次方程ax²+bx+c=n﹣1有两个不相等的实数根．
其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

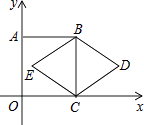
12. 2017⁰+2|1﹣sin30°|﹣（ $\frac{1}{3}$ ）^﹣¹+ $\sqrt{16}$ = ．

查看试题解析
13. 如图，正方形ABCO的顶点C、A分别在x轴、y轴上，BC是菱形BDCE的对角线，若∠D=60°，BC=2，则点D的坐标是．

查看试题解析
14. 对于实数a、b，定义一种新运算“⊗”为：a⊗b= $\frac{1}{a - b^{2}}$ ，这里等式右边是实数运算．例如：1⊗3= $\frac{1}{1 - 3^{2}}$ =﹣ $\frac{1}{8}$ ．则方程x⊗（﹣2）= $\frac{2}{x - 4}$ ﹣1的解是．

查看试题解析
15.
如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P₁（0，1），P₂（1，1），P₃（1，0），P₄（1，﹣1），P₅（2，﹣1），P₆（2，0），…，则点P₉₀的坐标是．

查看试题解析
16. 如图，在等边△ABC中，AB=4，点P是BC边上的动点，点P关于直线AB，AC的对称点分别为M，N，则线段MN长的取值范围是．

查看试题解析
17. 已知A、B、C、D是平面坐标系中坐标轴上的点，且△AOB≌△COD．设直线AB的表达式为y₁=k₁x+b₁ ，直线CD的表达式为y₂=k₂x+b₂ ，则k₁•k₂= ．

查看试题解析

三、解答题

18. 先化简，再求值：
（ $\frac{x}{x^{2} + x}$ ﹣1）÷ $\frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ，其中x的值从不等式组 ${\begin{cases} - x \leq 1 \\ 2 x - 1 < 4 \end{cases}$ 的整数解中选取．

查看试题解析
19.
如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）

(1)、请画出将△ABC向左平移4个单位长度后得到的图形△A₁B₁C₁；

(2)、请画出△ABC关于原点O成中心对称的图形△A₂B₂C₂；

(3)、在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标．

查看试题解析
20. 某新农村乐园设置了一个秋千场所，如图所示，秋千拉绳OB的长为3m，静止时，踏板到地面距离BD的长为0.6m（踏板厚度忽略不计）．为安全起见，乐园管理处规定：儿童的“安全高度”为hm，成人的“安全高度”为2m（计算结果精确到0.1m）

(1)、当摆绳OA与OB成45°夹角时，恰为儿童的安全高度，则h=m

(2)、某成人在玩秋千时，摆绳OC与OB的最大夹角为55°，问此人是否安全？（参考数据： $\sqrt{2}$ ≈1.41，sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）

查看试题解析
21. 如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD=2DB，AM=2MO，一次函数y=kx+b的图象过点D和M，反比例函数y= $\frac{m}{x}$ 的图象经过点D，与BC的交点为N．

(1)、求反比例函数和一次函数的表达式；

(2)、若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．

查看试题解析
22. 如图，AB为⊙O的直径，直线CD切⊙O于点M，BE⊥CD于点E．

(1)、求证：∠BME=∠MAB；

(2)、求证：BM²=BE•AB；

(3)、若BE= $\frac{18}{5}$ ，sin∠BAM= $\frac{3}{5}$ ，求线段AM的长．

查看试题解析
23.
如图，抛物线y=ax²+bx+c经过点A（﹣3，0），B（1，0），C（0，﹣3）．

(1)、求抛物线的解析式；

(2)、若点P为第三象限内抛物线上的一点，设△PAC的面积为S，求S的最大值并求出此时点P的坐标；

(3)、设抛物线的顶点为D，DE⊥x轴于点E，在y轴上是否存在点M，使得△ADM是直角三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

查看试题解析