浙江省宁波市余姚市2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2019-12-13 类型:期中考试
一、选择题(每小题3分,共36分)
-
1. 如图所示,下列图形中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如果一个三角形的两边长分别为3和6,则第三边长可能是( )A、1 B、3 C、6 D、93. 若x﹥y , 且(a-1) x<(a-1) y , 则a的值可能是( )A、 0 B、1 C、2 D、34. 下列各图中,正确画出AC边上的高的是( )A、
2. 如果一个三角形的两边长分别为3和6,则第三边长可能是( )A、1 B、3 C、6 D、93. 若x﹥y , 且(a-1) x<(a-1) y , 则a的值可能是( )A、 0 B、1 C、2 D、34. 下列各图中,正确画出AC边上的高的是( )A、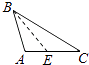 B、
B、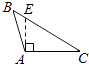 C、
C、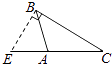 D、
D、 5. 下列条件中,能判定△ABC ≌ △DEF的是( )
5. 下列条件中,能判定△ABC ≌ △DEF的是( )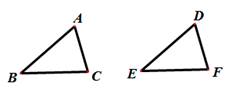 A、∠A=∠D , ∠B=∠E,∠C=∠F B、AC=DF , ∠B=∠E,BC=EF C、AB=DE , ∠B=∠E,AC=DF D、AB=DE , ∠B=∠E,BC=EF6. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、
A、∠A=∠D , ∠B=∠E,∠C=∠F B、AC=DF , ∠B=∠E,BC=EF C、AB=DE , ∠B=∠E,AC=DF D、AB=DE , ∠B=∠E,BC=EF6. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、 B、
B、  C、
C、  D、
D、  7. 下列命题中,它们的逆命题为真命题的是( )
7. 下列命题中,它们的逆命题为真命题的是( )①对顶角相等; ②内错角相等,两直线平行; ③若a=b ,则 ; ④等边三角形有一个角等于 60° .
A、①②③④ B、②③ C、③④ D、②8. 如图,已知△ABC(AB<BC<AC) , 用尺规在AC上确定一点P , 使PB+PC=AC , 则符合要求的作图痕迹是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在△ABC中,AB=AC , AD、CE分别是△ABC的中线和角平分线.若∠CAD=20° , 则∠ACE的度数是( )
9. 如图,在△ABC中,AB=AC , AD、CE分别是△ABC的中线和角平分线.若∠CAD=20° , 则∠ACE的度数是( ) A、55° B、40° C、35° D、20°10. 某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们.如果每人送3本,则还余8本;如果前面每人送5本,则最后一人得到了课外读物,但是不足3本.问:该校获奖的学生有( )A、5人 B、6人 C、7人 D、8人11. 如图,在6×6的正方形网格中,点A , B均在正方形格点上,若在网格中的格点上找一点C , 使△ABC为等腰三角形,这样的点C一共有( )
A、55° B、40° C、35° D、20°10. 某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们.如果每人送3本,则还余8本;如果前面每人送5本,则最后一人得到了课外读物,但是不足3本.问:该校获奖的学生有( )A、5人 B、6人 C、7人 D、8人11. 如图,在6×6的正方形网格中,点A , B均在正方形格点上,若在网格中的格点上找一点C , 使△ABC为等腰三角形,这样的点C一共有( )
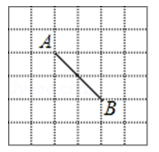
A、7个 B、8个 C、10个 D、12个12. 如图,在锐角△ABC中,AB=AC=8 , S△ABC=24 , 且AD⊥BC , 点P,Q分别是AB,AD上的动点,则BQ+PQ的最小值是( )
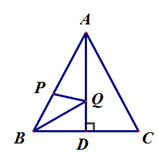
A、3 B、4 C、6 D、8二、填空题(每小题3分,共18分)
-
13. “x与y的2倍的和是正数”用不等式可表示为.14. 在△ABC中,AB=AC,∠A=50°,则∠C=.15. 关于 的不等式-2<x≤ a有3个整数解,则a的取值范围是.16. 如图,在△ABC中,AB=10cm , AC=6cm , BC=8cm , 点D、E分别在AB、AC上,且BD平分∠ABC , AC⊥BC , DE⊥AB , 垂足分别为C , E , 则△ADE的周长为 .
 17. 等腰三角形一腰上的高与另一腰所成的夹角为45°,则这个等腰三角形的顶角的度数为.18. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G , 过点G作EF∥BC交AB于E , 交AC于F , 过点G作GD⊥AC于D , 下列四个结论:①EF=BE+CF;②点G到△ABC各边的距离相等;③ ;④设GD=m , AE+AF=n , 则S△AEF=mn. 其中正确的结论有.
17. 等腰三角形一腰上的高与另一腰所成的夹角为45°,则这个等腰三角形的顶角的度数为.18. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G , 过点G作EF∥BC交AB于E , 交AC于F , 过点G作GD⊥AC于D , 下列四个结论:①EF=BE+CF;②点G到△ABC各边的距离相等;③ ;④设GD=m , AE+AF=n , 则S△AEF=mn. 其中正确的结论有.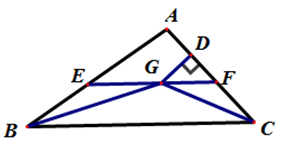
三、解答题(共66分)
-
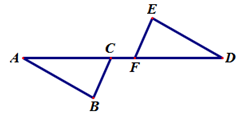
19.(1)、解不等式 ,并把所得解集表示在数轴上.(2)、解不等式组 ,并写出它的所有整数解.20. 如图,点A , C,F,D在同一条直线上,AB=DE , AF=DC , BC=EF , .试判断AB与CD的位置关系,并说明理由.
 21. 如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
21. 如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
⑴涂黑部分的面积是原正方形面积的一半;
⑵涂黑部分成轴对称图形.
如图乙是一种涂法,请在图1~3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图乙与图丙)
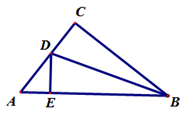
22. 如图,在△ABC中,点D在BC上,且AB=AC=BD , DA=DC. (1)、写出图中所有的等腰三角形;(2)、求∠B的度数.23. 已知:如图,AB∥CD , M是BC的中点,DM平分∠ADC .
(1)、写出图中所有的等腰三角形;(2)、求∠B的度数.23. 已知:如图,AB∥CD , M是BC的中点,DM平分∠ADC .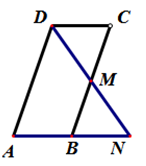 (1)、求证:△MCD≌△MBN ;(2)、试判断线段AB、AD、CD之间的数量关系,并说明理由.24. 2022年冬奥会和冬残奥会将在北京举行,前不久首批7家特许商品零售店在北京开业。经北京冬奥组委批准上市的特许商品包括徽章、钥匙扣等普通金属制品、金银条及贵金属纪念章、服装服饰、文具、陶瓷和纪念邮品等六大类商品。这些商品都由环保材料制作,充分体现了本届冬奥会绿色环保的承办理念。某余姚市市民想购买徽章和笔记本这两类纪念品,若购买2个徽章和3本笔记本需320元,且徽章的单价比笔记本单价多10元.(1)、求徽章和笔记本的单价各是多少元?(2)、该市民购买徽章和笔记本共8件,其中徽章的数量超过笔记本的数量,且总费用不超过550元,该市民有哪几种购买方案,并指出哪种购买方案所需资金最少?最少多少元?25. 如果一个三角形被一条线段分割成两个等腰三角形,那么这种分割叫做等腰分割,这条线段称为这个三角形的等腰分割线.如图1,当△ABD和△ACD为等腰三角形时,AD为△ABC的等腰分割线.
(1)、求证:△MCD≌△MBN ;(2)、试判断线段AB、AD、CD之间的数量关系,并说明理由.24. 2022年冬奥会和冬残奥会将在北京举行,前不久首批7家特许商品零售店在北京开业。经北京冬奥组委批准上市的特许商品包括徽章、钥匙扣等普通金属制品、金银条及贵金属纪念章、服装服饰、文具、陶瓷和纪念邮品等六大类商品。这些商品都由环保材料制作,充分体现了本届冬奥会绿色环保的承办理念。某余姚市市民想购买徽章和笔记本这两类纪念品,若购买2个徽章和3本笔记本需320元,且徽章的单价比笔记本单价多10元.(1)、求徽章和笔记本的单价各是多少元?(2)、该市民购买徽章和笔记本共8件,其中徽章的数量超过笔记本的数量,且总费用不超过550元,该市民有哪几种购买方案,并指出哪种购买方案所需资金最少?最少多少元?25. 如果一个三角形被一条线段分割成两个等腰三角形,那么这种分割叫做等腰分割,这条线段称为这个三角形的等腰分割线.如图1,当△ABD和△ACD为等腰三角形时,AD为△ABC的等腰分割线. (1)、如图2,△ABC中,∠B=2∠C , 线段AC的垂直平分线ED交AC于点D , 交BC于点E . 求证:AE是△ABC的一条等腰分割线.(2)、如图3,在△ABC中,∠A=120° , ∠B=20° , ∠C=40° , 请你完成△ABC的等腰分割,并在图中标注底角的度数.
(1)、如图2,△ABC中,∠B=2∠C , 线段AC的垂直平分线ED交AC于点D , 交BC于点E . 求证:AE是△ABC的一条等腰分割线.(2)、如图3,在△ABC中,∠A=120° , ∠B=20° , ∠C=40° , 请你完成△ABC的等腰分割,并在图中标注底角的度数. (3)、在△ABC中,BD为△ABC的等腰分割线,且AD=BD , ∠C=30° , 请你画出所有可能的图形并求出∠A的度数.26. 如图
(3)、在△ABC中,BD为△ABC的等腰分割线,且AD=BD , ∠C=30° , 请你画出所有可能的图形并求出∠A的度数.26. 如图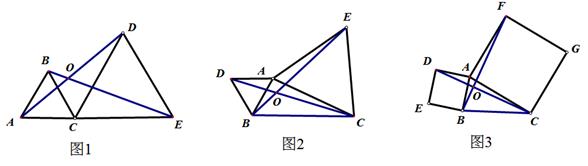 (1)、观察探索:
(1)、观察探索:如图1,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE , AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q , 连接PQ .
①求证:△ADC≌△BEC;②求∠BOA的度数.
(2)、类比探究:如图2,在△ABC中,分别以AB和AC为边向外作等边三角形(△ADB和△ACE),连接DC、BE , 交于点O.求∠BOD的度数.
(3)、深入推广:如图3,在△ABC中,分别以AB和AC为边向外作正方形(正方形ABED和正方形ACGF),连接DC、BE , 交于点O.请直接写出∠BOD的度数.