2017年山东省潍坊市中考数学二模试卷
试卷更新日期:2017-07-25 类型:中考模拟
一、选择题
-
1. 下列运算正确的是( )A、an•a2=a2n B、a3•a2=a6 C、an•(a2)n=a2n+2 D、a2n﹣3÷a﹣3=a2n2. 人工智能AlphaGo因在人机大战中大胜韩国围棋手李世石九段而声名显赫.它具有自我对弈学习能力,决战前已做了两千万局的训练(等同于一个人近千年的训练量).此处“两千万”用科学记数法表示为( )A、0.2×107 B、2×107 C、0.2×108 D、2×1083. 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
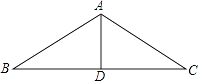 A、5sin36°米 B、5cos36°米 C、5tan36°米 D、10tan36°米4. 已知关于x的分式方程 + =1的解是非负数,则m的取值范围是( )A、m>2 B、m≥2 C、m≥2且m≠3 D、m>2且m≠35. 若关于x的方程x2﹣ +cosα=0有两个相等的实数根,则锐角α为( )A、30° B、45° C、60° D、75°6. 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是( )
A、5sin36°米 B、5cos36°米 C、5tan36°米 D、10tan36°米4. 已知关于x的分式方程 + =1的解是非负数,则m的取值范围是( )A、m>2 B、m≥2 C、m≥2且m≠3 D、m>2且m≠35. 若关于x的方程x2﹣ +cosα=0有两个相等的实数根,则锐角α为( )A、30° B、45° C、60° D、75°6. 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是( ) A、40π B、24π C、20 π D、12π7. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A、40π B、24π C、20 π D、12π7. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( ) A、35° B、40° C、50° D、65°8. 如图,矩形ABCD中,AB= ,BC= ,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则 等于( )
A、35° B、40° C、50° D、65°8. 如图,矩形ABCD中,AB= ,BC= ,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则 等于( ) A、 B、 C、 D、9. 二次函数y=﹣x2+1的图象与x轴交于A、B两点,与y轴交于点C,下列说法错误的是( )A、点C的坐标是(0,1) B、线段AB的长为2 C、△ABC是等腰直角三角形 D、当x>0时,y随x增大而增大10. 如图,⊙C过原点,与x轴、y轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则⊙C半径是( )
A、 B、 C、 D、9. 二次函数y=﹣x2+1的图象与x轴交于A、B两点,与y轴交于点C,下列说法错误的是( )A、点C的坐标是(0,1) B、线段AB的长为2 C、△ABC是等腰直角三角形 D、当x>0时,y随x增大而增大10. 如图,⊙C过原点,与x轴、y轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则⊙C半径是( ) A、 B、 C、 D、211. 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
A、 B、 C、 D、211. 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )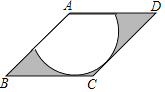 A、1﹣ B、 C、1﹣ D、12. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A、1﹣ B、 C、1﹣ D、12. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )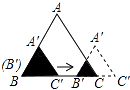 A、
A、 B、
B、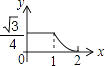 C、
C、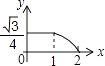 D、
D、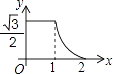
二、填空题
-
13. 分解因式:x2﹣y2﹣3x﹣3y=14. 计算 ﹣|2 ﹣2cos30°|+( )﹣1﹣(1﹣π)0的结果是 .15. 如图,已知函数y=ax+b与函数y=kx﹣3的图象交于点P(4,﹣6),则不等式ax+b≤kx﹣3<0的解集是 .
 16. 计算: = .17. 如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于 .
16. 计算: = .17. 如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于 . 18. 手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20= .
18. 手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20= .
三、解答题
-
19. 某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题
测量教学楼高度
方案
一
二
图示
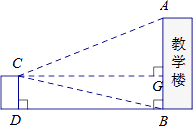
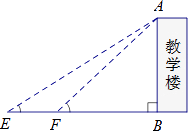
测得数据
CD=6.9m,∠ACG=22°,∠BCG=13°,
EF=10m,∠AEB=32°,∠AFB=43°
参考数据
sin22°≈0.37,cos22°≈0.93,
tan22°≈0.40
sin13°≈0.22,cos13°≈0.97
tan13°≈0.23
sin32°≈0.53,cos32°≈0.85,tan32°≈0.62
sin43°≈0.68,cos43°≈0.73,tan43°≈0.93
请你选择其中的一种方法,求教学楼的高度(结果保留整数)
20. 目前中学生带手机进校园现象越来越受到社会关注,针对这种现象,某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题: (1)、此次抽样调查中,共调查了多少名中学生家长;(2)、求出图2中扇形C所对的圆心角的度数,并将图1补充完整;(3)、根据抽样调查结果,请你估计1万名中学生家长中有多少名家长持反对态度;(4)、在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.21. 小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA﹣AB所示.
(1)、此次抽样调查中,共调查了多少名中学生家长;(2)、求出图2中扇形C所对的圆心角的度数,并将图1补充完整;(3)、根据抽样调查结果,请你估计1万名中学生家长中有多少名家长持反对态度;(4)、在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.21. 小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA﹣AB所示. (1)、试求折线段OA﹣AB所对应的函数关系式;(2)、请解释图中线段AB的实际意义;(3)、请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离s(千米)与小明出发后的时间t(分钟)之间函数关系的图象.(友情提醒:请对画出的图象用数据作适当的标注)22. LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
(1)、试求折线段OA﹣AB所对应的函数关系式;(2)、请解释图中线段AB的实际意义;(3)、请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离s(千米)与小明出发后的时间t(分钟)之间函数关系的图象.(友情提醒:请对画出的图象用数据作适当的标注)22. LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:LED灯泡
普通白炽灯泡
进价(元)
45
25
标价(元)
60
30
 (1)、该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?(2)、由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?23. 如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:
(1)、该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?(2)、由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?23. 如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形: (1)、当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;
(1)、当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由; (2)、当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).
(2)、当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论). 24. 如图,在Rt△ABC中,∠C=90°,sinA= ,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.
24. 如图,在Rt△ABC中,∠C=90°,sinA= ,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF. (1)、求证:DF为⊙O的切线;(2)、若AO=x,DF=y,求y与x之间的函数关系式.25.
(1)、求证:DF为⊙O的切线;(2)、若AO=x,DF=y,求y与x之间的函数关系式.25.如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣ x2+ x+4经过A、B两点.
 (1)、写出点A、点B的坐标;(2)、若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;(3)、在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、写出点A、点B的坐标;(2)、若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;(3)、在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.