浙江省宁波市鄞州区2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2019-12-13 类型:期中考试
一、单项选择题(每小题3分,共30分)
-
1. 国家宝藏 节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多观众走进博物馆,让一个个馆藏文物鲜活起来 下面四幅图是我国一些博物馆的标志,其中是轴对称图形的是A、
 B、
B、 C、
C、 D、
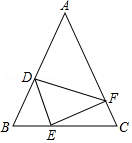
D、 2. 若三角形的两条边长分别为6cm和10cm,则它的第三边长不可能为( )A、5cm B、8cm C、10cm D、17cm3. 如果 ,那么下列不等式中正确的是A、 B、 C、 D、4. 下列命题是真命题的是A、三角形的三条高线相交于三角形内一点 B、等腰三角形的中线与高线重合 C、三边长为 , , 的三角形为直角三角形 D、到线段两端距离相等的点在这条线段的垂直平分线上5. 某实验室有一块三角形玻璃,被摔成如图所示的四块,胡老师想去店里买一块形状、大小与原来一样的玻璃,胡老师要带的玻璃编号是( )
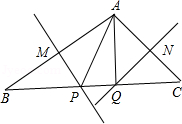
2. 若三角形的两条边长分别为6cm和10cm,则它的第三边长不可能为( )A、5cm B、8cm C、10cm D、17cm3. 如果 ,那么下列不等式中正确的是A、 B、 C、 D、4. 下列命题是真命题的是A、三角形的三条高线相交于三角形内一点 B、等腰三角形的中线与高线重合 C、三边长为 , , 的三角形为直角三角形 D、到线段两端距离相等的点在这条线段的垂直平分线上5. 某实验室有一块三角形玻璃,被摔成如图所示的四块,胡老师想去店里买一块形状、大小与原来一样的玻璃,胡老师要带的玻璃编号是( )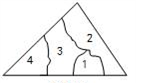 A、1 B、2 C、3 D、46. 若等腰三角形的一个内角为80°,则底角的度数为( )A、20° B、20°或50° C、80° D、50°或80°7. 如图, 中, , , 平分 交 于点 ,点 为 的中点,连接 ,则 的周长为
A、1 B、2 C、3 D、46. 若等腰三角形的一个内角为80°,则底角的度数为( )A、20° B、20°或50° C、80° D、50°或80°7. 如图, 中, , , 平分 交 于点 ,点 为 的中点,连接 ,则 的周长为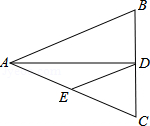 A、20 B、12 C、14 D、138. 现用甲、乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排( )
A、20 B、12 C、14 D、138. 现用甲、乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排( )
A、4辆 B、5辆 C、6辆 D、7辆9. 如图,折叠长方形纸片 的一边 ,使点 落在 边上的点 处,已知 , ,则折痕 的长为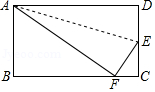 A、 B、 C、 D、1310. 关于 的不等式组 有四个整数解,则 的取值范围是A、 B、 C、 D、
A、 B、 C、 D、1310. 关于 的不等式组 有四个整数解,则 的取值范围是A、 B、 C、 D、二、填空题:(每小题3分,共30分)
-
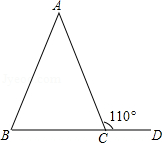
11. 在 中, , ,则 .12. 用不等式表示:x的两倍与3的差不小于5,则这个不等式是.13. 如图,在 中, ,外角 ,则 .
 14. 如图,点 在 的平分线上,若使 ,则需添加的一个条件是 (只写一个即可,不添加辅助线).
14. 如图,点 在 的平分线上,若使 ,则需添加的一个条件是 (只写一个即可,不添加辅助线).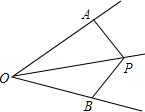 15. 已知关于 的不等式组 的解集为 ,则 的值为16. 小颖准备用10元钱买笔记本和作业本,已知每本笔记本1.8元,每本作业本0.6元,她买了3本笔记本,你帮她算一算,她最多还可以买本作业本.17. 如图,小巷左右两侧是竖直的墙,已知小巷的宽度是2.2米,一架梯子斜靠在左墙时,梯子底端到坐墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端距离地面米.
15. 已知关于 的不等式组 的解集为 ,则 的值为16. 小颖准备用10元钱买笔记本和作业本,已知每本笔记本1.8元,每本作业本0.6元,她买了3本笔记本,你帮她算一算,她最多还可以买本作业本.17. 如图,小巷左右两侧是竖直的墙,已知小巷的宽度是2.2米,一架梯子斜靠在左墙时,梯子底端到坐墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端距离地面米.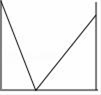 18. 如图,在 中, 和 的平分线相交于点 ,过点 作 交 于 ,交 于 ,过点 作 于 ,下列三个结论:① ;② ;③点 到 各边的距离相等;其中正确的结论有(填序号)
18. 如图,在 中, 和 的平分线相交于点 ,过点 作 交 于 ,交 于 ,过点 作 于 ,下列三个结论:① ;② ;③点 到 各边的距离相等;其中正确的结论有(填序号)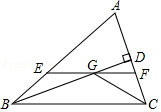 19. 如图, 中, 为 的中点, ,垂足为 .若 , ,则 的长度是 .
19. 如图, 中, 为 的中点, ,垂足为 .若 , ,则 的长度是 .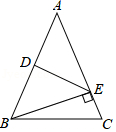 20. 如图, , 内有一定点 ,且 ,在 上有一点 , 上有一点 ,若 周长最小, 则最小周长是
20. 如图, , 内有一定点 ,且 ,在 上有一点 , 上有一点 ,若 周长最小, 则最小周长是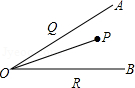
三、解答题(本题有6小题,共40分)
-
21. 解不等式组: ,并把解集在数轴上表示出来.
 22. 如图,在 中, , 是 的平分线, ,交 于点 .
22. 如图,在 中, , 是 的平分线, ,交 于点 .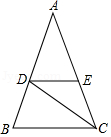 (1)、求证: .(2)、若 ,求 的度数.23. 对于任意实数 定义关于 的一种运算如下: 例如:(1)、若 求 的取值范围;(2)、已知关于 的方程 的解满足 求 的取值范围.24. 如图, 中, ,若 和 分别垂直平分 和 , , ,求 的长.
(1)、求证: .(2)、若 ,求 的度数.23. 对于任意实数 定义关于 的一种运算如下: 例如:(1)、若 求 的取值范围;(2)、已知关于 的方程 的解满足 求 的取值范围.24. 如图, 中, ,若 和 分别垂直平分 和 , , ,求 的长.