浙江省嘉兴市秀洲区、经开区七校联考2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-13 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 下列事件中,属于必然事件的为A、打开电视机,正在播放广告 B、任意画一个三角形,它的内角和等于 C、掷一枚硬币,正面朝上 D、在只有红球的盒子里摸到白球2. 从分别写有数字1,2,3,4,5,6的6张质地、大小完全一样的卡片中随机抽取一张,抽取的卡片上的数是3的倍数的概率是A、 B、 C、 D、3. 抛物线把抛物线 向右平移2个单位,则所得抛物线的表达式为A、 B、 C、 D、4. 如图, 是 的外接圆, ,则 的度数为
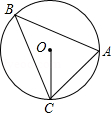 A、 B、 C、 D、5. 下列命题中,是真命题的是A、三点确定一个圆 B、相等的圆周角所对的弧相等 C、平分弦的直径垂直于弦 D、 的圆周角所对的弦是直径6. 半径为5的 ,圆心在直角坐标系的原点 ,则点 与 的位置关系是A、在 上 B、在 内 C、在 外 D、不能确定7. 二次函数 经过点 、 和 ,则下列说法正确的是A、抛物线的开口向下 B、当 时, 随 的增大而增大 C、二次函数的最小值是 D、抛物线的对称轴是直线8. 嘉兴南湖不仅是党的诞生地,它优美的风光还吸引全国各地的旅客前来观赏.如图是南湖的一座三孔桥,某天测得最大桥拱的水面宽 为 ,桥顶 到水面 的距离为 ,则这座桥桥拱半径为
A、 B、 C、 D、5. 下列命题中,是真命题的是A、三点确定一个圆 B、相等的圆周角所对的弧相等 C、平分弦的直径垂直于弦 D、 的圆周角所对的弦是直径6. 半径为5的 ,圆心在直角坐标系的原点 ,则点 与 的位置关系是A、在 上 B、在 内 C、在 外 D、不能确定7. 二次函数 经过点 、 和 ,则下列说法正确的是A、抛物线的开口向下 B、当 时, 随 的增大而增大 C、二次函数的最小值是 D、抛物线的对称轴是直线8. 嘉兴南湖不仅是党的诞生地,它优美的风光还吸引全国各地的旅客前来观赏.如图是南湖的一座三孔桥,某天测得最大桥拱的水面宽 为 ,桥顶 到水面 的距离为 ,则这座桥桥拱半径为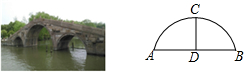 A、 B、 C、 D、9. 一个正五边形和一个正六边形按如图方式摆放,它们都有一边在直线 上,且有一个公共顶点 ,则 的度数是
A、 B、 C、 D、9. 一个正五边形和一个正六边形按如图方式摆放,它们都有一边在直线 上,且有一个公共顶点 ,则 的度数是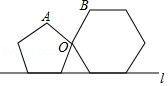 A、 B、 C、 D、10. 如图,等腰 的直角边与正方形 的边长均为2,且 与 在同一直线上,开始时点 与点 重合,让 沿这条直线向右平移,直到点 与点 重合为止.设 的长为 , 与正方形 重合部分(图中阴影部分)的面积为 ,则 与 之间的函数关系的图象大致是
A、 B、 C、 D、10. 如图,等腰 的直角边与正方形 的边长均为2,且 与 在同一直线上,开始时点 与点 重合,让 沿这条直线向右平移,直到点 与点 重合为止.设 的长为 , 与正方形 重合部分(图中阴影部分)的面积为 ,则 与 之间的函数关系的图象大致是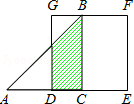 A、
A、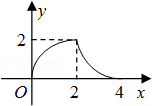 B、
B、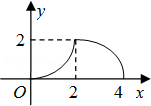 C、
C、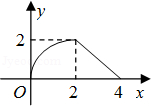 D、
D、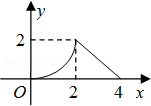
二、填空题(本题有10小题,每小题3分,共30分)
-
11. 二次函数 的顶点坐标是 .12. 在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有3个红球,每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在0.25左右,则白球的个数约为 .13. 抛物线 上有两点 和 ,则 和 的大小关系为 .14. 已知扇形的圆心角为 ,面积为 ,则该扇形所在圆的半径为 .15. 的两直角边长分别为6和8,则该 的外接圆的半径为 .16. 若 为 的一条弦, ,点 为该 上异于 , 的一点,则 度数是 .17. 如图,四边形 内接于圆 , 为边 延长线上一点,已知弧 的度数为 ,则 .
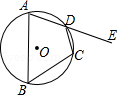 18. 如图,将 绕点 顺时针旋转一定的角度至 处,使得点 恰好在线段 上,若 ,则旋转角度数为 .
18. 如图,将 绕点 顺时针旋转一定的角度至 处,使得点 恰好在线段 上,若 ,则旋转角度数为 . 19. 在直角坐标系中,抛物线 交 轴于点 ,点 是点 关于对称轴的对称点,点 是抛物线的顶点,若 的外接圆经过原点 ,则 的值为 .
19. 在直角坐标系中,抛物线 交 轴于点 ,点 是点 关于对称轴的对称点,点 是抛物线的顶点,若 的外接圆经过原点 ,则 的值为 .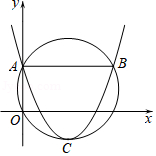 20. 已知抛物线 与 轴只有一个交点,以下四个结论:①该抛物线的对称轴在 轴左侧;②关于 的方程 有实数根;③ ;④ .其中结论正确的为 .
20. 已知抛物线 与 轴只有一个交点,以下四个结论:①该抛物线的对称轴在 轴左侧;②关于 的方程 有实数根;③ ;④ .其中结论正确的为 .三、解答题(本题有6小题,共40分)
-
21. 如图,正方形网格中(每个小正方形的边长都为1个单位),在平面直角坐标系内, 的顶点 、 分别为 , .
 (1)、画出 绕点 逆时针旋转 后的△ ;(2)、在(1)的条件下,求出旋转过程中点 所经过的路径长(结果保留 .22. 2019年第六届世界互联网大会在桐乡乌镇召开,某校九年级选拔了3名男生和2名女生参加某分会场的志愿者工作.本次学生志愿者工作一共设置了三个岗位,分别是引导员、联络员和咨询员.(1)、若要从这5名志愿者中随机选取一位作为引导员,求选到女生的概率;(2)、若甲、乙两位志愿者都从三个岗位中随机选择一个,请你用画树状图或列表法求出他们恰好选择同一个岗位的概率.(画树状图和列表时可用字母代替岗位名称)23. 如图,直线 和抛物线 都经过点 、点 ,且 ,
(1)、画出 绕点 逆时针旋转 后的△ ;(2)、在(1)的条件下,求出旋转过程中点 所经过的路径长(结果保留 .22. 2019年第六届世界互联网大会在桐乡乌镇召开,某校九年级选拔了3名男生和2名女生参加某分会场的志愿者工作.本次学生志愿者工作一共设置了三个岗位,分别是引导员、联络员和咨询员.(1)、若要从这5名志愿者中随机选取一位作为引导员,求选到女生的概率;(2)、若甲、乙两位志愿者都从三个岗位中随机选择一个,请你用画树状图或列表法求出他们恰好选择同一个岗位的概率.(画树状图和列表时可用字母代替岗位名称)23. 如图,直线 和抛物线 都经过点 、点 ,且 ,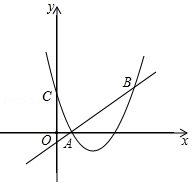 (1)、求 的值及点 的坐标;(2)、求不等式 的解集.(直接写出答案)24. 如图,已知 是 的直径, , 是 上的点, ,交 于点 ,连结 .
(1)、求 的值及点 的坐标;(2)、求不等式 的解集.(直接写出答案)24. 如图,已知 是 的直径, , 是 上的点, ,交 于点 ,连结 .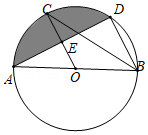 (1)、求证: ;(2)、若 , ,求图中阴影部分的面积.25. 某商场要经营一种新上市的文具,进价为20元 件.试营销阶段发现:当销售单价是25元时,每天的销售量为150件;销售单价每上涨1元,每天的销售量就减少10件.设销售单价为 (元 ,每天的销售量为 (件 ,每天所得的销售利润 (元 .(1)、求出 与 之间的函数关系式;(2)、求出 与 之间的函数关系式,并求当销售单价为多少元时,该文具每天的销售利润最大,最大利润为多少?26. 已知,抛物线 的图象经过点 , .
(1)、求证: ;(2)、若 , ,求图中阴影部分的面积.25. 某商场要经营一种新上市的文具,进价为20元 件.试营销阶段发现:当销售单价是25元时,每天的销售量为150件;销售单价每上涨1元,每天的销售量就减少10件.设销售单价为 (元 ,每天的销售量为 (件 ,每天所得的销售利润 (元 .(1)、求出 与 之间的函数关系式;(2)、求出 与 之间的函数关系式,并求当销售单价为多少元时,该文具每天的销售利润最大,最大利润为多少?26. 已知,抛物线 的图象经过点 , .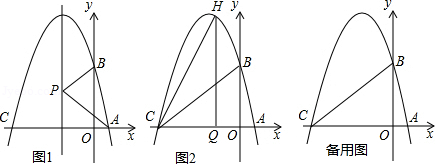 (1)、求这个抛物线的解析式;(2)、如图1, 是抛物线对称轴上一点,连接 , ,试求出当 的值最小时点 的坐标;(3)、如图2, 是线段 上的一点,过点 作 轴,与抛物线交于 点,若直线 把 分成面积之比为 的两部分,请求出 点的坐标.
(1)、求这个抛物线的解析式;(2)、如图1, 是抛物线对称轴上一点,连接 , ,试求出当 的值最小时点 的坐标;(3)、如图2, 是线段 上的一点,过点 作 轴,与抛物线交于 点,若直线 把 分成面积之比为 的两部分,请求出 点的坐标.