浙教版2019-2020学年初中数学七年级上学期期末复习专题5 图形的初步认识 提高训练
试卷更新日期:2019-12-12 类型:复习试卷
一、单选题
-
1. 如图,已知直线AB,CD,EF相交于点O,OG平分∠BOD,则图中对顶角(小于180°的角)有______对( )
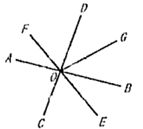 A、3 B、5 C、6 D、82. 如图, 于点 ,过点 作直线 ,使 .则 的度数为( )
A、3 B、5 C、6 D、82. 如图, 于点 ,过点 作直线 ,使 .则 的度数为( )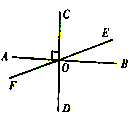 A、22.5° B、77.5° C、67.5° D、60°3. 如图,在直线l上依次有A,B,C三点,则图中线段共有( )
A、22.5° B、77.5° C、67.5° D、60°3. 如图,在直线l上依次有A,B,C三点,则图中线段共有( ) A、4 条 B、3 条 C、2 条 D、1 条4. 如图,将一副三角尺按不同位置摆放,摆放方式中 与 互余的是( )A、
A、4 条 B、3 条 C、2 条 D、1 条4. 如图,将一副三角尺按不同位置摆放,摆放方式中 与 互余的是( )A、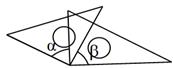 B、
B、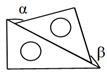 C、
C、 D、
D、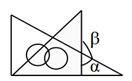 5. 下列图形中能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )A、
5. 下列图形中能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )A、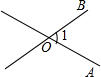 B、
B、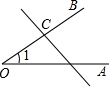 C、
C、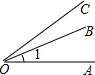 D、
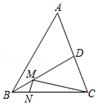
D、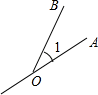 6. 如图,在锐角三角形ABC中,BC=4,∠ABC=60°,BD平分∠ABC , 交AC于点D , M , N分别是BD , BC上的动点,
6. 如图,在锐角三角形ABC中,BC=4,∠ABC=60°,BD平分∠ABC , 交AC于点D , M , N分别是BD , BC上的动点,则CM+MN的最小值是( )
 A、 B、2 C、2 D、47. 已知∠α是锐角,∠β是钝角,且∠α+∠β=180°,那么下列结论正确的是( )A、 的补角和 的补角相等 B、 的余角和 的补角相等 C、 的余角和 的补角互余 D、 的余角和 的补角互补8. 如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD= AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
A、 B、2 C、2 D、47. 已知∠α是锐角,∠β是钝角,且∠α+∠β=180°,那么下列结论正确的是( )A、 的补角和 的补角相等 B、 的余角和 的补角相等 C、 的余角和 的补角互余 D、 的余角和 的补角互补8. 如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD= AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )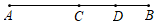 A、 B、 C、 D、9. 已知点C是线段AB延长线上的一点,M、N分别是线段AB、AC的中点,若MN=4cm,且AB= AC,则线段AC的长为( )cmA、24 B、32 C、40 D、4810. 已知线段AB=8,延长线段AB至C,使得BC= AB,延长线段BA至D,使得AD= AB,则下列判断正确的是( )A、BC= AD B、BD=3BC C、BD=4AD D、AC=6AD
A、 B、 C、 D、9. 已知点C是线段AB延长线上的一点,M、N分别是线段AB、AC的中点,若MN=4cm,且AB= AC,则线段AC的长为( )cmA、24 B、32 C、40 D、4810. 已知线段AB=8,延长线段AB至C,使得BC= AB,延长线段BA至D,使得AD= AB,则下列判断正确的是( )A、BC= AD B、BD=3BC C、BD=4AD D、AC=6AD二、填空题
-
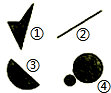
11. 由平面上的点组成图形A,如果连接A中任意两点的线段必定在A内,则称A为平面上的凸图形.给出如图所示的平面上的4个图形(阴影区域及其边界),其中为凸图形的是(写出所有凸图形的序号)
 12. 如图所示,已知AB、CD相交与O,OE平分∠AOD,OF⊥CD于O,∠1=40°,则∠2=;∠3=.
12. 如图所示,已知AB、CD相交与O,OE平分∠AOD,OF⊥CD于O,∠1=40°,则∠2=;∠3=.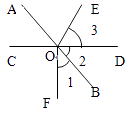 13. 如图,点C是线段AB上一点,AC<CB,M、N分别是AB和CB的中点,AC=8,NB=5,则线段MN=.
13. 如图,点C是线段AB上一点,AC<CB,M、N分别是AB和CB的中点,AC=8,NB=5,则线段MN=.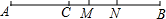 14. 如图,已知OA⊥OB,点O为垂足,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC与∠BOD互余,其中正确的有(只填写正确结论的序号).
14. 如图,已知OA⊥OB,点O为垂足,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC与∠BOD互余,其中正确的有(只填写正确结论的序号).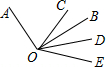 15. 已知线段AB,点C、点D在直线AB上,并且CD=8,AC:CB=1:2,BD:AB=2:3,则AB=.16. 如图1,OP为一条拉直的细线,长为7cm,A,B两点在OP上,若先握住点B,将OB折向BP,使得OB重叠在BP上,如图 再从图2的A点及与A点重叠处一起剪开,使得细线分成三段 若这三段的长度由短到长之比为1:2:4,其中以点P为一端的那段细线最长,则OB的长为cm.
15. 已知线段AB,点C、点D在直线AB上,并且CD=8,AC:CB=1:2,BD:AB=2:3,则AB=.16. 如图1,OP为一条拉直的细线,长为7cm,A,B两点在OP上,若先握住点B,将OB折向BP,使得OB重叠在BP上,如图 再从图2的A点及与A点重叠处一起剪开,使得细线分成三段 若这三段的长度由短到长之比为1:2:4,其中以点P为一端的那段细线最长,则OB的长为cm.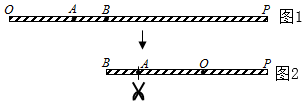
三、解答题
-
17. 已知线段 ,在线段AB上有点C,D,M,N四个点,且满足AC:CD: :2:4, ,且 ,求MN的长.18. 如图,已知点A、B、C、D,根据下列语句画图(保留画图痕迹):
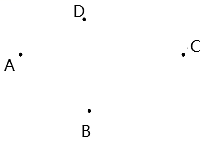 (1)、画射线AC;(2)、连接AB、BC、BD,线段BD与射线AC交于点O;(3)、①在线段AC上作一条线段CF,使得
(1)、画射线AC;(2)、连接AB、BC、BD,线段BD与射线AC交于点O;(3)、①在线段AC上作一条线段CF,使得②观察图形,我们发现线段AB+BC>AC,得出这个结论的依据是.
19. 如图所示,直线AB,CD相交于点O,P是CD上一点.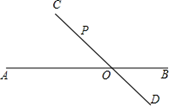 (1)、①过点P画AB的垂线段PE.
(1)、①过点P画AB的垂线段PE.②过点P画CD的垂线,与AB相交于F点.
(2)、说明线段PE,PO,FO三者的大小关系,其依据是什么?20. 如图,P是线段AB上任一点,AB=12cm,C、D两点分别从P、B同时向A点运动,且C点的运动速度为2cm/s,D点的运动速度为3cm/s,运动的时间为ts. (1)、若AP=8cm,
(1)、若AP=8cm,①运动1s后,求CD的长;
②当D在线段PB上运动时,试说明AC=2CD;
(2)、如果t=2s时,CD=1cm,试探索AP的值.21. 如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的三倍,则称射线OC是∠AOB的“奇分线”,如图2,∠MPN=42°: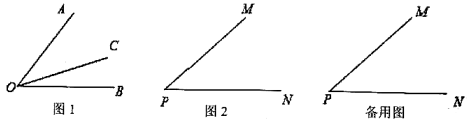 (1)、过点P作射线PQ,若射线PQ是∠MPN的“奇分线”,求∠MPQ;(2)、若射线PE绕点P从PN位置开始,以每秒8°的速度顺时针旋转,当∠EPN首次等于180°时停止旋转,设旋转的时间为 (秒).当 为何值时,射线PN是∠EPM的“奇分线”?22. 如图,已知线段AB=a.延长线段BA到点C,使AC=2AB,延长线段AB到点E,使BE= BC.
(1)、过点P作射线PQ,若射线PQ是∠MPN的“奇分线”,求∠MPQ;(2)、若射线PE绕点P从PN位置开始,以每秒8°的速度顺时针旋转,当∠EPN首次等于180°时停止旋转,设旋转的时间为 (秒).当 为何值时,射线PN是∠EPM的“奇分线”?22. 如图,已知线段AB=a.延长线段BA到点C,使AC=2AB,延长线段AB到点E,使BE= BC. (1)、用刻度尺按要求补全图形;(2)、图中有几条线段?求出所有线段的长度和(用含a的代数式表示);(3)、点D是CE的中点,若AD=0.5cm,求a的值.23. 如图,E是直线AC上一点,EF是∠AEB的平分线.
(1)、用刻度尺按要求补全图形;(2)、图中有几条线段?求出所有线段的长度和(用含a的代数式表示);(3)、点D是CE的中点,若AD=0.5cm,求a的值.23. 如图,E是直线AC上一点,EF是∠AEB的平分线.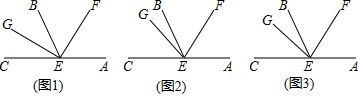 (1)、如图1,若EG是∠BEC的平分线,求∠GEF的度数;(2)、如图2,若GE在∠BEC内,且∠CEG=3∠BEG,∠GEF=75°,求∠BEG的度数.(3)、如图3,若GE在∠BEC内,且∠CEG=n∠BEG,∠GEF=α,求∠BEG(用含n、α的代数式表示).24. O为直线AB上的一点,OC⊥OD,射线OE平分∠AOD.
(1)、如图1,若EG是∠BEC的平分线,求∠GEF的度数;(2)、如图2,若GE在∠BEC内,且∠CEG=3∠BEG,∠GEF=75°,求∠BEG的度数.(3)、如图3,若GE在∠BEC内,且∠CEG=n∠BEG,∠GEF=α,求∠BEG(用含n、α的代数式表示).24. O为直线AB上的一点,OC⊥OD,射线OE平分∠AOD. (1)、如图①,判断∠COE和∠BOD之间的数量关系,并说明理由;(2)、若将∠COD绕点O旋转至图②的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;(3)、若将∠COD绕点O旋转至图③的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.
(1)、如图①,判断∠COE和∠BOD之间的数量关系,并说明理由;(2)、若将∠COD绕点O旋转至图②的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;(3)、若将∠COD绕点O旋转至图③的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.