浙教版2019-2020学年初中数学七年级上学期期末复习专题4 一元一次方程 提高训练
试卷更新日期:2019-12-12 类型:复习试卷
一、单选题
-
1. 如果 是关于x的一元一次方程,则m的值为A、4 B、 C、2 D、2或2. 下列结论错误的是( )A、若a=b,则 B、若 ,则a=b C、若x=3,则x2=3x D、若ax+2=bx+2,则a=b3. 若关于 的方程 的解是整数,则整数 的取值个数是( )A、 B、 C、 D、4. 小聪按如图所示的程序输入一个正数x,最后输出的结果为853,则满足条件的x的不同值最多有( )
 A、4个 B、5个 C、6个 D、无数个5. 在排成每行七天的月历表中取下一个 方块(如图所示).若所有日期数之和为189,则n的值为( )
A、4个 B、5个 C、6个 D、无数个5. 在排成每行七天的月历表中取下一个 方块(如图所示).若所有日期数之和为189,则n的值为( )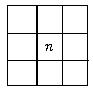 A、21 B、11 C、15 D、96. 某商贩在一次买卖中,同时卖出两件上衣,售价都是 元,若按成本计,其中一件盈利 ,另一件亏本 ,在这次买卖中他( ).A、赔8元 B、不赚不赔 C、赔16元 D、赚16元7. 将正整数 1 至 1050 按一定规律排列如下表:
A、21 B、11 C、15 D、96. 某商贩在一次买卖中,同时卖出两件上衣,售价都是 元,若按成本计,其中一件盈利 ,另一件亏本 ,在这次买卖中他( ).A、赔8元 B、不赚不赔 C、赔16元 D、赚16元7. 将正整数 1 至 1050 按一定规律排列如下表:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
从表中任取一个 3× 3 的方框(如表中带阴影的部分),方框中九个数的和可能是( )
A、2025 B、2018 C、2016 D、20078. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、 B、 C、 D、9. 把1400元的奖金按两种奖给22名学生,其中一等奖每人200元,二等奖每人50元,设获一等奖的学生有x人,则下列方程错误的是( )A、200x+50(22-x)=1400 B、 C、50x+200×(22-x)=1400 D、(200-50)x+50×22=140010. 某商场根据市场信息,对商场中现有的两台不同型号的空调进行调价销售,其中一台空调调价后售出可获利 (相对于进价),另一台空调调价后售出则亏本20%(相对于进价),而这两台空调调价后的售价恰好相同,那么商场把这两台空调调价后售出( )A、要亏本 B、可获利 C、要亏本2% D、既不获利也不亏本二、填空题
-
11. 在数学活动课上,老师说有人根据如下的证明过程,得到“1=2”的结论.
设a、b为正数,且a=b.
∵a=b,
∴ab=b2 . ①
∴ab﹣a2=b2﹣a2 . ②
∴a(b﹣a)=(b+a)(b﹣a). ③
∴a=b+a.④
∴a=2a.⑤
∴1=2.⑥
大家经过认真讨论,发现上述证明过程中从某一步开始出现错误,这一步是(填入编号),造成错误的原因是 .
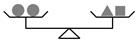
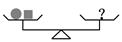
12. 若|a+1|+|a﹣2|=5,|b﹣2|+|b+3|=7,则a+b= .13. 一个两位数,个位数字与十位数字的和是9,如果将个位数字与十位数字对调后所得的新数比原数大9,则原来的两位数是。14. 甲、乙两点在边长为100m的正方形ABCD上按顺时针方向运动,甲的速度为5m/秒,乙的速度为10m/秒,甲从A点出发,乙从CD边的中点出发,则经过秒,甲乙两点第一次在同一边上.15. 如下图有三个平衡的天平,请问第三个天平“?”处放个▲.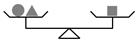
 16. 父亲带着两个儿子向离家33千米的奶奶家出发,父亲有一辆摩托车,速度为25千米 小时,如果再载了另一个人,则速度为20千米 小时 摩托车不允许带两个人,即每车至多载两人 每个儿子如果步行速度为5千米 小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为小时.
16. 父亲带着两个儿子向离家33千米的奶奶家出发,父亲有一辆摩托车,速度为25千米 小时,如果再载了另一个人,则速度为20千米 小时 摩托车不允许带两个人,即每车至多载两人 每个儿子如果步行速度为5千米 小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为小时.三、解答题
-
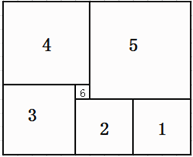
17. 解方程:(1)、10x﹣12=5x+15;(2)、18. 解下列方程:(1)、2x+5=3(x-1)(2)、(3)、(4)、 x+2 =8+x.19. 请你阅读下面的诗句并解答:“栖树一群鸦,鸦树不知数,三只栖一树,五只没去处,五只栖一树,闲了一棵树,请你仔细数,鸦树各几何?”20. 一个长方形如图所示,恰好分成六个正方形。其中中间最小的一个正方形边长为1,求这个长方形的面积.
 21. 用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.如:1*3=1×32+2×1×3+1=16.(1)、求2*(-2)的值;
21. 用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.如:1*3=1×32+2×1×3+1=16.(1)、求2*(-2)的值;
(2)、若2*x=m,( x)*3=n(其中x为有理数),试比较m,n的大小;(3)、若[ *(-3)]* =a+4,求a的值.22. 光华中学库存若干套桌椅,准备修理后支援贫困山区学校.现有甲、乙两修理组,甲修理组单独完成任务需要12天,乙修理组单独完成任务需要24天.(1)、若由甲、乙两修理组同时修理,需多少天可以修好这些套桌椅?(2)、若甲、乙两修理组合作3天后,甲修理组因新任务离开,乙修理组继续工作.甲完 成新任务后,回库与乙又合作3天,恰好完成任务.问:甲修理组离开几天?(3)、学校需要每天支付甲修理组、乙修理组修理费分别为80元,120元.任务完成后, 两修理组收到的总费用为1920元,求甲修理组修理了几天?23. 甲,乙两人沿湖边环形道上匀速跑步,他们开启了微信运动﹣﹣微信上实时统计每天步数的软件.已知乙的步距比甲的步距少0.4m(步距是指每一步的距离),且每2分钟甲比乙多跑25步,两人各跑3周后到达同一地点,跑3圈前后的时刻和步数如下:出发时刻
出发时微信运动中显示的步数
结束时刻
结束时微信运动中显示的步数
甲
9:30
2158
9:40
4158
乙
a
1308
9:40
4308
(1)、求甲,乙的步距和环形道的周长;(2)、求表中a的值;(3)、若两人于9:40开始反向跑,问:此后,当微运动中显示的步数相差50步时,他们相遇了几次?24. 为庆祝“6.1”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装价格表:购买服装的套数
1套--45套
46套--90套
91套及以上
每套服装的价格
60元
50元
40元
如果两所学校分别单独购买服装,一共应付5000元.
(1)、如果甲、乙两校联合购买服装,那么比各自购买服装共可以节省多少钱?(2)、甲乙两校各有多少学生准备参加演出?(3)、如果甲校有10名同学抽调去参加书法绘画比赛半年参加演出,请为两校设计一种省钱的购买服装方案.